题目内容
(本小题满分12分)在平面直角坐标系中,点 在角
在角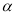 的终边上,点
的终边上,点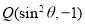 在角
在角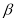 的终边上,且
的终边上,且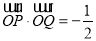 .
.
(1)求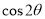 的值;(2)求
的值;(2)求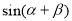 的值.
的值.
(1) ,(2)
,(2)
【解析】
试题分析:首先利用平面向量数量积公式(坐标运算),表示出 ,求出
,求出 ,进而利用二倍角公式求出
,进而利用二倍角公式求出 ;第二步利用第一步求出的
;第二步利用第一步求出的 和
和 的值找出
的值找出 两点坐标,写出
两点坐标,写出 以及
以及 ,最终求出
,最终求出 .
.
试题解析:(1)因为 ,所以
,所以 ,
,
即: ,所以
,所以 ,
,
所以 .
.
(2)因为 ,所以
,所以 ,所以
,所以 ,
, ,
,
又点 在角
在角 的终边上,所以
的终边上,所以
同理 
所以:
考点:1.平面向量的数量积;2.二倍角公式;3.两角和、差公式
考点分析: 考点1:三角恒等变换 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
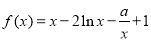 ,
,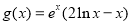 .
.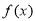 在定义域上是增函数,求a的取值范围;
在定义域上是增函数,求a的取值范围; 的最大值.
的最大值. ;命题q:
;命题q: ,函数
,函数 的图象过点
的图象过点 ,则( )
,则( ) 上存在点
上存在点 满足约束条件
满足约束条件 则实数
则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 , 集合
, 集合 ,
,  , 则集合
, 则集合 可以表示为( )
可以表示为( ) B.
B.
 D.
D.
 ,
, ,若
,若 与
与 共线,则实数
共线,则实数 的值是 .
的值是 . 中,若
中,若 ,
, ,
, 的
的 项和为
项和为 ,则
,则 ( )
( ) B.2 C.
B.2 C. D.
D.
 的图象大致为( )
的图象大致为( )
 的解集为
的解集为 ,则一元一次不等式
,则一元一次不等式 的解集为 .
的解集为 .