题目内容
9．已知函数f（x）=$\frac{{2}^{x}-1}{{2}^{x}+1}$ 对任意的x∈R，不等式f（x）＜a恒成立，求a的取值范围．分析 先将原函数分离常数，然后结合指数函数的性质，再求含有自变量部分的式子的范围，则问题可解．
解答 解：由已知原函数可化为：$f（x）=\frac{{2}^{x}+1-2}{{2}^{x}+1}=1-\frac{2}{{2}^{x}+1}$．
因为2x＞0，所以2x+1＞1，
所以0$＜\frac{2}{{2}^{x}+1}＜2$，所以$-2＜-\frac{2}{{2}^{x}+1}＜0$，
所以$-1＜1-\frac{2}{{2}^{x}+1}＜1$，
所以要使对任意的x∈R，不等式f（x）＜a恒成立，
只需a≥1即可．
故所求a的范围是[1，+∞）．
点评 本题考查了指数函数的性质，不等式恒成立问题转化为函数最值问题的解题思路．
练习册系列答案
相关题目
17．若将函数y=2sin（4x+φ）的图象向右平移$\frac{π}{6}$个单位，得到的图象关于y轴对称，则|ϕ|的最小值是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{5}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{3}$ |
如图，在平面直角坐标系xOy中，已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点，点D（1，0），点P，B在椭圆上，$\overrightarrow{BP}$=$\overrightarrow{DA}$．
14．已知点P在曲线y=$\frac{4}{{（2}^{x}+1）ln2}$上，α为曲线在点P处的切线的倾斜角，则α的取值范围是．
| A． | [0，$\frac{π}{4}$） | B． | [$\frac{π}{4}$，$\frac{π}{2}$） | C． | （$\frac{π}{2}$，$\frac{3}{4}$π] | D． | [$\frac{3}{4}$π，π） |
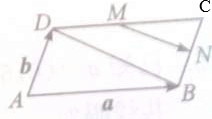如图，?ABCD中，M、N分别是边DC、BC的中点．