题目内容
(文)如图,在棱长为4的正方体ABCD—A′B′C′D′中,E、F分别是AD、A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′?上运动,则线段MN的中点P的轨迹(曲面)与二面角A-A′D′-B′所围成的几何体的体积为( )
A. B. C. D.
C
解析试题分析:因为点M在定长的线段EF上运动,那么另一个端点在底面A′B′C′D′?上运动,因此可知,在运动中有一个不变量,就是点F到线段MN中点的距离始终为斜边的一半,也就是1,则可知中点的轨迹是四分之一个球面,那么与二面角所围城的体积为四分之一个球体的体积,因此半径为1,则根据球体的体积公式可知 ,故选C.
,故选C.
考点:本试题考查了轨迹方程与空间几何体的结合体的运用。
点评:解决该试题的关键是能准确的表示出点的轨迹方程,进而确定出轨迹形状,利用几何图形和二面角所围城的图形来求解其体积。属于难度试题。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
已知三棱锥的底面是边长为 的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为
的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为
A. | B. | C. | D. |
棱长为1的正方体的外接球的表面积为
A. | B. | C. | D. |
已知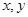 满足
满足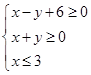 ,若
,若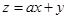 的最大值为
的最大值为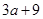 ,最小值为
,最小值为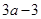 ,则a的范围为 ( )
,则a的范围为 ( )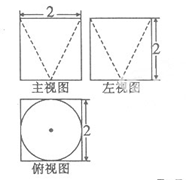
A.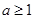 | B.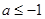 | C.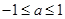 | D.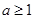 或 或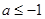 |
已知一个几何体的三视图如图所示,则该几何体的体积是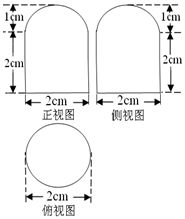
A. | B. |
C. | D. |
已知圆锥的底面半径为1,且它的侧面展开图是一个半圆,则这个圆锥的体积为( )
A.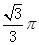 | B.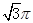 | C.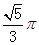  | D.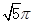 |
一个几何体的三视图如图所示,则该几何体的表面积
| A.38-π | B.38 | C.38+π | D.38-2π |
右图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的侧视图的面积为( )
A.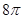 | B.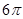 | C.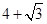 | D.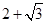 |
如图,四棱锥S—ABCD的底面为正方形,SD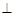 底面ABCD,则下列结论中不正确的是
底面ABCD,则下列结论中不正确的是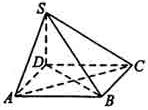
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D.AB与SC所成的角等于DC与SA所成的角 |