题目内容
已知对任意q
都有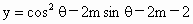 恒小于0,求实数m的取值范围.
恒小于0,求实数m的取值范围.
答案:略
解析:
解析:
|
解:  ,y恒小于0. ,y恒小于0.
又 
∵- 1≤sinq ≤1.(1)当-1≤m≤1时,若sinq =-m, 则 由题意,设 又-1≤m≤1,所以 (2)当m>1时,若sinq
=-1,则 (3)当m<-1时,若sinq
=1,则 由题意,设-4m-2<0,即 综上可得,m的取值范围是 |

练习册系列答案
相关题目
已知函数 的一系列对应值如下表:
的一系列对应值如下表:
(1)根据表格提供的数据求函数y=f(x)的解析式;
(2)(文)当x∈[0,2π]时,求方程f(x)=2B的解.
(3)(理)若对任意的实数a,函数y=f(kx)(k>0), 的图象与直线y=1有且仅有两个不同的交点,又当
的图象与直线y=1有且仅有两个不同的交点,又当 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
 的一系列对应值如下表:
的一系列对应值如下表:| x |  |  |  |  |  |  |  |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
(2)(文)当x∈[0,2π]时,求方程f(x)=2B的解.
(3)(理)若对任意的实数a,函数y=f(kx)(k>0),
 的图象与直线y=1有且仅有两个不同的交点,又当
的图象与直线y=1有且仅有两个不同的交点,又当 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
已知函数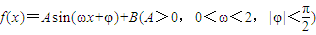 的一系列对应值如下表:
的一系列对应值如下表:
(1)根据表格提供的数据求函数y=f(x)的解析式;
(2)(文)当x∈[0,2π]时,求方程f(x)=2B的解.
(3)(理)若对任意的实数a,函数y=f(kx)(k>0),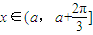 的图象与直线y=1有且仅有两个不同的交点,又当
的图象与直线y=1有且仅有两个不同的交点,又当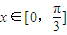 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
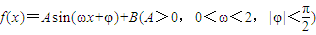 的一系列对应值如下表:
的一系列对应值如下表:| x | 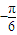 | 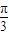 | 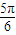 | 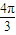 | 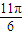 | 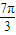 | 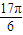 |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
(2)(文)当x∈[0,2π]时,求方程f(x)=2B的解.
(3)(理)若对任意的实数a,函数y=f(kx)(k>0),
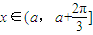 的图象与直线y=1有且仅有两个不同的交点,又当
的图象与直线y=1有且仅有两个不同的交点,又当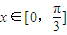 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围. ,
, ,得
,得 .
. ;
; 恒成立,所以mÎ
(1,+∞);
恒成立,所以mÎ
(1,+∞); .
. ,与m<-1矛盾,所以mÎ
Æ
.
,与m<-1矛盾,所以mÎ
Æ
. .
. 恒小于0,求实数m的取值范围.
恒小于0,求实数m的取值范围. 恒小于0,求实数m的取值范围.
恒小于0,求实数m的取值范围.