题目内容
设函数f（x）=sin（wx+φ），其中|φ|＜
．若f（-
）≤f（x）≤f（
）对任意x∈R恒成立，则正数w的最小值为________，此时，φ=________．
2 -
分析：直接利用函数的周期的最大值，即可求解ω的最小值．通过函数的最大值求出φ
解答：因为函数f（x）=sin（ωx+φ），其中|φ|＜．若f（-）≤f（x）≤f（）对任意x∈R恒成立，
所以
的最大值为：
，所以正数ω的最小值为：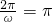
，ω=2，
因为函数的最大值为f（），
所以2×
=，所以φ=
，
故答案为：2，．
点评：本题考查三角函数的解析式的求法，函数的基本性质的应用，考查分析问题解决问题的能力．
分析：直接利用函数的周期的最大值，即可求解ω的最小值．通过函数的最大值求出φ
解答：因为函数f（x）=sin（ωx+φ），其中|φ|＜
．若f（-）≤f（x）≤f（）对任意x∈R恒成立，所以
的最大值为：，所以正数ω的最小值为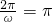：，ω=2，因为函数的最大值为f（
），所以2×
=，所以φ=，故答案为：2，
．点评：本题考查三角函数的解析式的求法，函数的基本性质的应用，考查分析问题解决问题的能力．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目