题目内容
【题目】已知函数f（x）=x|x+a|﹣ 
lnx．
（1）当a=0时，讨论函数f（x）的单调性；
（2）若a＜0，讨论函数f（x）的极值点．
【答案】
（1）解：当a=0时，f（x）=x2﹣ 
lnx，函数的定义域为（0，+∞）．
f′（x）= 
，
令f′（x）＞0，可得x＞ ，f′（x）＞0，可得0＜x＜ ，
∴函数f（x）的单调增区间是（ ，+∞），单调减区间是（0， ）
（2）解：当a＜0时，f（x）=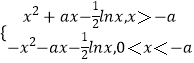 
．
①x＞﹣a时，f′（x）= 
=0，可得x1= 
，x2= 
＜﹣a（舍去）．
若 ≤﹣a，即a≤﹣ 
，f′（x）≥0，∴函数f（x）在（﹣a，+∞）上单调递增；
若 ＞﹣a，即﹣ ＜a＜0，则当x∈（﹣a，x1）时，f′（x）＜0，x∈（x1，+∞），f′（x）＞0，
∴f（x）在∈（﹣a，x1）上单调递减，在（x1，+∞）上单调递增．
②当0＜x＜﹣a时，f′（x）= 
=0，得﹣4x2﹣2ax﹣1=0．
记△=4a2﹣16．
△≤0，即﹣2≤a＜0，f′（x）≤0，∴f（x）在（0，﹣a）上单调递减；
△＞0，即a＜﹣2，f′（x）=0可得x3= 
，x4= 且0＜x3＜x4＜﹣a．
x∈（0，x3）时，f′（x）＜0，x∈（x3，x4）时，f′（x）＞0，x∈（x4，﹣a），f′（x）＜0，
∴f（x）在（0，x3）上单调递减，在（x3，x4）上单调递增，在（x4，﹣a）上单调递减，
综上所述，a＜﹣2时，f（x）的极小值点为 ，极大值点为 
；﹣2≤a≤﹣ 时，f（x）无极值点；
﹣ ＜a＜0时，f（x）的极小值点为
【解析】（1）当a=0时，f（x）=x2﹣ lnx，函数的定义域为（0，+∞），求导数，断导数的符号，即可判断f（x）的单调性；（2）分类讨论，利用极值的定义，即可讨论函数f（x）的极值点．
【考点精析】认真审题，首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减)，还要掌握函数的极值与导数(求函数的极值的方法是:（1）如果在
附近的左侧
,右侧
,那么
是极大值（2）如果在附近的左侧,右侧
,那么
是极小值)的相关知识才是答题的关键．
