题目内容

已知⊙C1:x2+y2-2mx+4y+m2-5=0,⊙C2:x2+y2+2x-2my+m2-3=0,当m为何值时,⊙C1和⊙C2(1)相离;(2)外切;(3)相交;(4)内切;(5)内含?

解析：将两圆化为标准方程,求出圆心和半径,运用圆心距|C1C2|与两半径r1,r2之间的关系判断.?

⊙C1:(x-m)2+(y+2)2=9,C1(m,-2),r1=3;?

⊙C2:(x+1)2+(y-m)2=4,C2(-1,m),r2=2.?

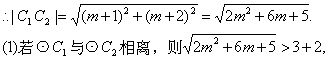
∴m＜-5或m＞2.

(2)若⊙C1与⊙C2外切,则＝3＋2

∴m=-5或m=2.?

(3)若⊙C1与⊙C2相交,则＜3+2,

∴-5＜m＜-2或-1＜m＜2.?

(4)若⊙C1与⊙C2内切,则=3-2,?

∴m=-2或m=-1.?

(5)若⊙C1与⊙C2内含,则＜3-2,?

∴-2＜m＜-1.

练习册系列答案
相关题目
给出下列命题：
①已知椭圆
x2
16
+
y2
8
=1的两个焦点为F1，F2，则这个椭圆上存在六个不同的点M，使得△F1MF2为直角三角形；
②已知直线l过抛物线y=2x2的焦点，且与这条抛物线交于A，B两点，则|AB|的最小值为2；
③若过双曲线C：
x2
a2
-
y2
b2
=1(a＞0，b＞0)的一个焦点作它的一条渐近线的垂线，垂足为M，O为坐标原点，则|OM|=a；
④已知⊙C1：x2+y2+2x=0，⊙C2：x2+y2+2y-1=0，则这两个圆恰有2条公切线．
其中正确命题的序号是
 
．（把你认为正确命题的序号都填上）
已知⊙C1：x2+（y+5）2=5，点A（1，-3）
（Ⅰ）求过点A与⊙C1相切的直线l的方程；
（Ⅱ）设⊙C2为⊙C1关于直线l对称的圆，则在x轴上是否存在点P，使得P到两圆的切线长之比为
2
？荐存在，求出点P的坐标；若不存在，试说明理由．
已知焦点在y轴上的椭圆C1：
y2
a2
+
x2
b2
=1经过A（1，0）点，且离心率为
3
2
．
（I）求椭圆C1的方程；
（Ⅱ）过抛物线C2：y=x2+h（h∈R）上P点的切线与椭圆C1交于两点M、N，记线段MN与PA的中点分别为G、H，当GH与y轴平行时，求h的最小值．
已知⊙C1：x2+（y+2）2=1，⊙C2：(x+
3
)2+(y-1)2=1；坐标平面内的点P满足：存在过点P的无穷多对夹角为60°的直线l1和l2，它们分别与⊙C1和⊙C2相交，且l1被⊙C1截得的弦长和l2被⊙C2截得的弦长相等．请你写出所有符合条件的点P的坐标：
（
3
，1）；（-2
3
，-2）
（
3
，1）；（-2
3
，-2）
．
已知C1：x2-8x+y2+15=0，C2：(x-t)2+(y-kt+2)2=1，若?t∈R，使得C1与C2至少有一个公共点，则k的取值范围
[0，
4
3
]
[0，
4
3
]
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网