题目内容
已知四边形ABCD为平行四边形,BC⊥平面ABE,AE⊥BE,BE = BC = 1,AE =  ,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点。
,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点。
(1)求证:MN⊥EA;
(2)求四棱锥M – ADNP的体积。
(1)利用线面垂直的性质定理来证明线线垂直,主要是对于 的证明。(2)1
的证明。(2)1
解析试题分析:解:方法一:
(Ⅰ)取 中点
中点 ,连接
,连接 ,
,


又 平面
平面 ,
, 平面
平面 ,
,
又 又
又 平面
平面
 ,
,

(Ⅱ)过 作
作 于
于 ,连接
,连接
 平面
平面 ,
,
又 平面
平面 ,
,
又
 平面
平面

 ,又
,又 ,
, 平面
平面 ,
,
 二面角
二面角 为二面角
为二面角 的平面角
的平面角
在 中,
中,


 二面角的余弦值为
二面角的余弦值为

方法二:
(Ⅰ) 平面
平面 平面
平面 ,
, 平面
平面 平面
平面 ,
,
过 作
作 平面
平面 ,则
,则
以 分别为
分别为 轴,
轴, 轴,
轴, 轴建立空间直角坐标系
轴建立空间直角坐标系


 ,
,

(Ⅱ) ,
, ,设
,设 为平面
为平面 的一个法向量
的一个法向量
 为满足题意的一组解
为满足题意的一组解

 ,
, ,设
,设

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 是正三角形,
是正三角形, 和
和 都垂直于平面
都垂直于平面 ,且
,且 ,
, 是
是 的中点.
的中点.
 平面
平面 .
. 
 是双曲线
是双曲线

 上一点,
上一点, 、
、 分别是双曲线
分别是双曲线 的左、右顶点,直线
的左、右顶点,直线 ,
, 的斜率之积为
的斜率之积为 .
.
 ,
, 两点,
两点, 为坐标原点,
为坐标原点, 为双曲线上一点,满足
为双曲线上一点,满足 ,求
,求 的值.
的值. 平面ABCD,AE=EB=BC=2,F为CE上的点,且BF
平面ABCD,AE=EB=BC=2,F为CE上的点,且BF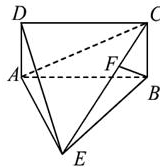
 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
 G是EF的中
G是EF的中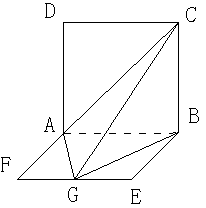
 中,
中, ,
, ,点
,点 在
在 上,
上, 交
交 于
于 ,
, 交
交 于
于 .沿
.沿 将△
将△ 翻折成△
翻折成△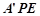 ,使平面
,使平面 平面
平面 将△
将△ 翻折成△
翻折成△ ,使平面
,使平面 平面
平面
 平面
平面 ,当
,当 为何值时,二面角
为何值时,二面角 的大小为
的大小为 ?
?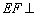 平面AEB,
平面AEB, ,
, ,
,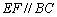 ,
,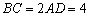 ,
,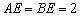 ,
, ,G是BC的中点.
,G是BC的中点.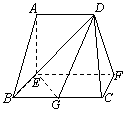
 ;
; 的大小.
的大小. 是正三角形,AB
是正三角形,AB 平面BCD,
平面BCD, ,E为BC的中点,F在棱AC上,且
,E为BC的中点,F在棱AC上,且
