题目内容
设函数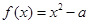 .
.
(1)求函数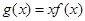 在区间
在区间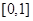 的最小值;
的最小值;
(2)当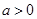 时,记曲线
时,记曲线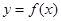 在
在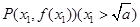 处的切线为
处的切线为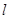 ,
,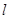 与
与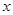 轴交于点
轴交于点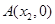 ,求证:
,求证: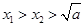 .
.
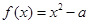 .
.(1)求函数
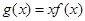 在区间
在区间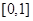 的最小值;
的最小值;(2)当
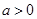 时,记曲线
时,记曲线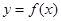 在
在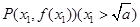 处的切线为
处的切线为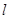 ,
,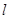 与
与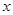 轴交于点
轴交于点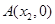 ,求证:
,求证: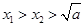 .
.见解析.
(1)先求出导数,再利用导数求最值的步骤求出最值,注意对参数a 的讨论要全面;(2)先求出切线方程,进一步求出点的坐标,然后利用不等式知识比较大小即可。
解:(1)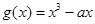 ,
,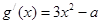 (2分)
(2分)
当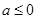 时,
时, 为
为 上的增函数
上的增函数
∴ 在区间
在区间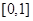 上的最小值为
上的最小值为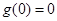 (4分)
(4分)
当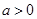 时,
时, 在
在 ,
, 上单调递增,在
上单调递增,在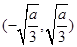 上单调递减
上单调递减
当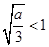 ,即
,即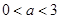 时,
时, 在区间
在区间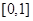 上的最小值为
上的最小值为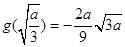
当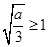 ,即
,即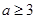 时,
时, 在区间
在区间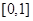 上的最小值为
上的最小值为 (8分)
(8分)
综上,当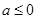 时,
时, 在区间
在区间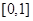 上的最小值为
上的最小值为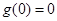 ;当
;当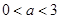 时,
时, 在区间
在区间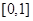 上的最小值为
上的最小值为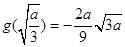 ;当
;当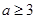 时,
时, 在区间
在区间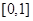 上的最小值为
上的最小值为 。
。
(II)证明:曲线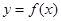 在点
在点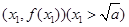 处的切线方程为:
处的切线方程为:
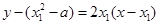 ,令
,令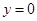 ,得
,得 (10分)
(10分)
∴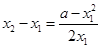 ,∵
,∵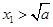 ,∴
,∴ ,
,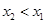 (12分)
(12分)
∵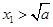 ,∴
,∴ ,∴
,∴
∴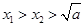 (15分)
(15分)
解:(1)
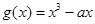 ,
,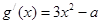 (2分)
(2分)当
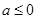 时,
时, 为
为 上的增函数
上的增函数∴
 在区间
在区间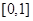 上的最小值为
上的最小值为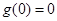 (4分)
(4分)当
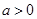 时,
时, 在
在 ,
, 上单调递增,在
上单调递增,在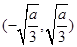 上单调递减
上单调递减 当
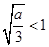 ,即
,即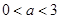 时,
时, 在区间
在区间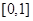 上的最小值为
上的最小值为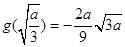
当
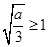 ,即
,即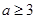 时,
时, 在区间
在区间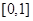 上的最小值为
上的最小值为 (8分)
(8分)综上,当
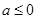 时,
时, 在区间
在区间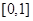 上的最小值为
上的最小值为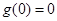 ;当
;当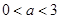 时,
时, 在区间
在区间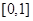 上的最小值为
上的最小值为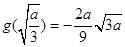 ;当
;当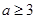 时,
时, 在区间
在区间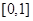 上的最小值为
上的最小值为 。
。(II)证明:曲线
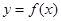 在点
在点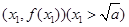 处的切线方程为:
处的切线方程为: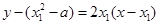 ,令
,令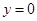 ,得
,得 (10分)
(10分)∴
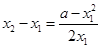 ,∵
,∵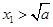 ,∴
,∴ ,
,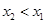 (12分)
(12分)∵
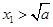 ,∴
,∴ ,∴
,∴
∴
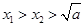 (15分)
(15分)
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
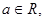 函数
函数 。
。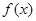 在区间
在区间 上最小值
上最小值 ;
;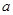 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数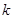 的取值范围;
的取值范围;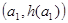 ,B
,B ,C
,C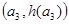 ,从左到右依次是函数
,从左到右依次是函数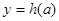 图象上三点,且这三点不共线,求证:
图象上三点,且这三点不共线,求证: 是钝角三角形。
是钝角三角形。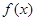 是定义在区间
是定义在区间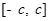 (
(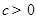 )上的奇函数,令
)上的奇函数,令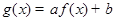 ,并有关于函数
,并有关于函数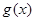 的四个论断:
的四个论断: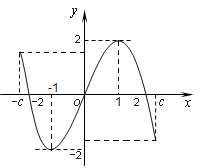
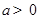 ,对于
,对于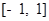 内的任意实数
内的任意实数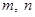 (
(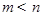 ),
),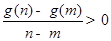 恒成立;
恒成立;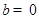 ;
;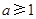 ,
,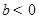 ,则方程
,则方程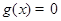 必有3个实数根;
必有3个实数根;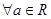 ,
,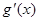 有两个零点;
有两个零点; 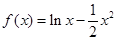 的大致图像是( )
的大致图像是( ) 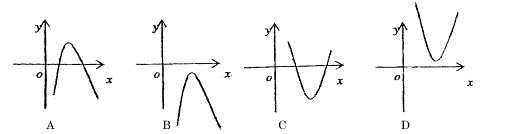
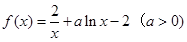 .
.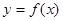 在点
在点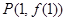 处的切线与直线
处的切线与直线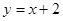 垂直,求函数
垂直,求函数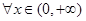 都有
都有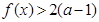 成立,试求
成立,试求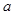 的取值范围;
的取值范围;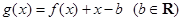 .当
.当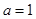 时,函数
时,函数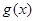 在区间
在区间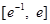 上有两个零点,求实数
上有两个零点,求实数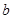 的取值范围.
的取值范围.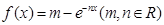
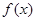 在点x=0处的切线方程为y=x,求m,n的值。
在点x=0处的切线方程为y=x,求m,n的值。 求a的取值范围.
求a的取值范围.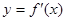 的图象可能为( )
的图象可能为( )
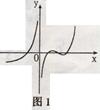 .
.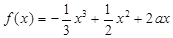 在区间
在区间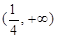 上存在单调递增区间,则的取值范围是
上存在单调递增区间,则的取值范围是 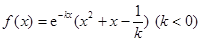 .
.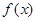 的单调区间;
的单调区间;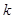 ,使得函数
,使得函数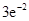 ?若存在,求出
?若存在,求出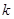 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.