题目内容
已知复数z满足|z-4|=|z-4i|,且z+
解:∵z+![]() ∈R,∴z+
∈R,∴z+![]() =
=![]() .
.
∴(z-![]() )[1-
)[1-![]() ]=0.
]=0.
从而z=![]() 或1-
或1-![]() =0,
=0,
即z∈R或|z-1|2=13.
由|z-4|=|z-4i|知复数z对应的点到复平面上两点(4,0)、(0,4)的距离相等.
∴复数z所对应的点在直线y=x上.
(1)若z∈R设z=x+yi,则y=0.
由![]() 得x=y=0,∴z=0.
得x=y=0,∴z=0.
(2)若|z-1|2=13,则z对应的点又在圆|z-1|=![]() 上,其直角坐标系中的方程为(x-1)2+y2=13.
上,其直角坐标系中的方程为(x-1)2+y2=13.
由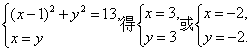
∴z=3+3i或z=-2-2i.
综上(1)(2),有z=0或z=3+3i或z=-2-2i.

练习册系列答案
相关题目
 ;
;