题目内容

设a＞b＞0，a+b=1，且x=logab，y=log(
1
a
+
1
b
)ab，z=log
1
b
a，则x、y、z之间的大小关系为（　　）
分析：由a＞b＞0，a+b=1可得0＜a＜1，0＜b＜1，从而可判断x＞1，y=-1，-1＜z＜0，问题解决．
解答：解：∵a＞b＞0，a+b=1
∴0＜a＜1，0＜b＜1，
∴logab＞logaa=1，又x=logab，
∴x＞1，y=
lgab
lg
a+b
ab
=-1，z=-
1
logab
＞-1，又z＜0，
∴y＜z＜x．
故选C．
点评：本题考查对数值大小的比较，关键在于对条件的转化，得到0＜a＜1，0＜b＜1，着重考查函数的单调性与求值，属于中档题．
练习册系列答案
相关题目
设
a
、
b
、
c
是任意的非零平面向量，且相互不共线，则
①(
a
•
b
)•
c
-(
c
•
a
)•
b
=
0
；
②|
a
|-|
b
|＜|
a
-
b
|；
③(
b
•
c
)
a
-(
c
•
a
)
b
不与
c
垂直；
④(3
a
+2
b
)•(3
a
-2
b
)=9|
a
|2-4|
b
|2中是真命题的有
 
．
1、设a，b∈R，若a-|b|＞0，则下列不等式中正确的是（　　）
（2012•江西模拟）有下面四个判断：
①命题：“设a、b∈R，若a+b≠6，则a≠3或b≠3”是一个假命题
②若“p或q”为真命题，则p、q均为真命题
③命题“?a、b∈R，a2+b2≥2（a-b-1）”的否定是：“?a、b∈R，a2+b2≤2（a-b-1）”
④若函数f(x)=ln(a+
2
x+1
)的图象关于原点对称，则a=3
其中正确的个数共有（　　）
设
a
、
b
为平面向量，若存在不全为零的实数λ，μ使得λ
a
+μ
b
=0，则称
a
、
b
线性相关，下面的命题中，
a
、
b
、
c
均为已知平面M上的向量．
①若
a
=2
b
，则
a
、
b
线性相关；
②若
a
、
b
为非零向量，且
a
⊥
b
，则
a
、
b
线性相关；
③若
a
、
b
线性相关，
b
、
c
线性相关，则
a
、
c
线性相关；
④向量
a
、
b
线性相关的充要条件是
a
、
b
共线．
上述命题中正确的是
 
（写出所有正确命题的编号）
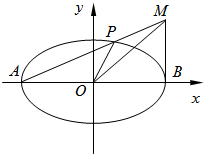精英家教网如图，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)，A、B是长轴的左、右端点，动点M满足MB⊥AB，联结AM，交椭圆于点P．
（1）当a=2，b=
2
时，设M（2，2），求
OP
•
OM
的值；
（2）若
OP
•
OM
为常数，探究a、b满足的条件？并说明理由；
（3）直接写出
OP
•
OM
为常数的一个不同于（2）结论类型的几何条件．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网