题目内容
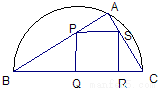
21、如图，△ABC的外接圆的切线AE与BC的延长线相交于点E，∠BAC的平分线与BC交于点D．求证：ED2=EB•EC．
分析：根据已知EA是圆的切线，AC为过切点A的弦得两个角相等，再结合角平分线条件，从而得到△EAD是等腰三角形，再根据切割线定理即可证得．
解答：证明：因为EA是圆的切线，AC为过切点A的弦，
所以∠CAE=∠CBA．
又因为AD是?BAC的平分线，所以∠BAD=∠CAD
所以∠DAE=∠DAC+∠EAC=∠BAD+∠CBA=∠ADE
所以，△EAD是等腰三角形，所以EA=ED．
又EA2=EC•EB，
所以ED2=EB•EC．
所以∠CAE=∠CBA．又因为AD是?BAC的平分线，所以∠BAD=∠CAD
所以∠DAE=∠DAC+∠EAC=∠BAD+∠CBA=∠ADE
所以，△EAD是等腰三角形，所以EA=ED．
又EA2=EC•EB，
所以ED2=EB•EC．
点评：此题主要是运用了弦切角定理的切割线定理．注意：切线长的平方应是EB和EC的乘积．
练习册系列答案
相关题目
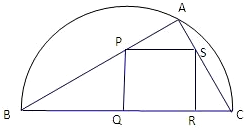如图，某小区准备绿化一块直径为BC的半圆形空地，△ABC外的地方种草，△ABC的内接正方形PQRS为一水池，其余地方种花．若BC=20米，∠ABC=θ，设△ABC的面积为S1，正方形PQRS的面积为S2，将比值
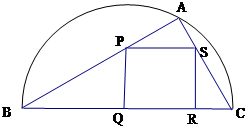如图，某小区准备绿化一块直径为BC的半圆形空地，△ABC的内接正方形PQRS为一水池，△ABC外的地方种草，其余地方种花．若BC=a，∠ABC=θ，设△ABC的面积为S1，正方形PQRS的面积为S2，将比值
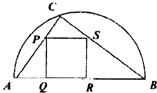如图，某小区准备绿化一块直径为AB的半圆形空地，点C在半圆弧上，半圆内△ABC外的地方种草，△ABC的内接正方形PQRS内部为一水池，其余地方种花，若AB=2a，∠CAB=θ，设△ABC的面积为S1，正方形PQRS的边长为x，面积为S2，将比值
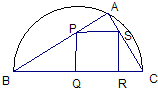（2007•杨浦区二模）如图，某小区准备绿化一块直径为BC的半圆形空地，△ABC外的地方种草，△ABC的内接正方形PQRS为一水池，其余地方种花．若BC=a，∠ABC=θ，设△ABC的面积为S1，正方形PQRS的面积为S2，将比值
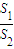称为“规划合理度”．