题目内容
AB是圆O的直径，PA垂直于圆O所在平面，C是圆周上任一点，设∠BAC=θ，PA=AB=2r，求异面直线PB和AC的距离．分析：异面直线PB和AC的距离可看成求直线PB上任意一点到AC的距离的最小值，从而设定变量，建立目标函数而求函数最小值．
解答：解：在PB上任取一点M，作MD⊥AC于D，MH⊥AB于H，
设MH=x，则MH⊥平面ABC，AC⊥HD．
∴MD2=x2+[（2r-x）sinθ]2=（sin2+1）x2-4rsin2θx+4r2sin2θ=（sin2θ+1）[x-
]2+
即当x=
时，MD取最小值
为两异面直线的距离．
由A、B、C成等差数列，可得B=60°；
由△ABC中tanA+tanB+tanC=tanA•tanB•tanC，得
tanA+tanC=tanB（tanA•tanC-1）=
（1+
）
设tanA、tanC是方程x2-（
+3）x+2+
=0的两根，解得x1=1，x2=2+
设A＜C，则tanA=1，tanC=2+
，∴A=
，C=
由此容易得到a=8，b=4
，c=4
+4．
设MH=x，则MH⊥平面ABC，AC⊥HD．
∴MD2=x2+[（2r-x）sinθ]2=（sin2+1）x2-4rsin2θx+4r2sin2θ=（sin2θ+1）[x-
| 2rsin2θ |
| 1+sin2θ |
| 4r2sin2θ |
| 1+sin2θ |
即当x=
| 2rsin2θ |
| 1+sin2θ |
| 2rsinθ | ||
|
由A、B、C成等差数列，可得B=60°；
由△ABC中tanA+tanB+tanC=tanA•tanB•tanC，得
tanA+tanC=tanB（tanA•tanC-1）=
| 3 |
| 3 |
设tanA、tanC是方程x2-（
| 3 |
| 3 |
| 3 |
设A＜C，则tanA=1，tanC=2+
| 3 |
| π |
| 4 |
| 5π |
| 12 |
由此容易得到a=8，b=4
| 6 |
| 3 |
点评：本题主要考查了点线面间的距离计算，函数思想的应用．考查了学生综合分析问题和基本的运算能力．
练习册系列答案
相关题目
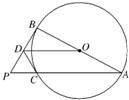如图，AB是圆O的直径，P为圆外一点，PB是圆O的切线，PA是圆O的割线且与圆O相交于点C．过点C作圆O的切线与PB交于D点．求证：
（2013•西城区一模）如图，已知AB是圆O的直径，P在AB的延长线上，PC切圆O于点C，CD⊥OP于D．若CD=6，CP=10，则圆O的半径长为
（2013•滨州一模）如图，AB是圆O的直径，P是圆弧
（2011•西城区二模）如图，AB是圆O的直径，P在AB的延长线上，PD切圆O于点C．已知圆O半径为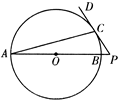
（1）如图，AB是圆O的直径，P在AB的延长线上，PD切圆O于点C．已知圆O半径为y=x-1（1≤x≤2），OP=2，则PC=