题目内容
已知数列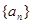 的前
的前 项和
项和 ,数列
,数列 满足
满足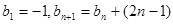
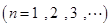 .
.
(1)求数列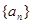 的通项
的通项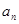 ;
;
(2)求数列 的通项
的通项 ;
;
(3)若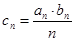 ,求数列
,求数列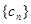 的前
的前 项和
项和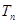 .
.
(1) (2)
(2) (3)
(3)
解析试题分析:(1)利用数列的前 项和
项和 与第
与第 项
项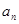 的关系
的关系 求解.
求解.
(2)由

又 可转化为等差数列前
可转化为等差数列前 项和问题.
项和问题.
(3)由(1)(2)可得
所以,
根据和式的特点可考虑用错位相减法解决.
试题解析:(1)∵ ,
,
∴ . 2分
. 2分
∴ . 3分
. 3分
当 时,
时, ,
,
∴ 4分
4分
(2)∵
∴ ,
,

 ,
,
以上各式相加得:

 9分
9分
(3)由题意得
∴ ,
,
∴ ,
,
∴

= ,
,
∴ . 12分
. 12分
考点:1、数列前 项和
项和 与第
与第 项
项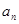 的关系;2、等差数列前
的关系;2、等差数列前 项和;3、错位相减法求数列前
项和;3、错位相减法求数列前 项和.
项和.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
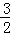 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.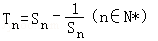 ,求数列{Tn}的最大项的值与最小项的值.
,求数列{Tn}的最大项的值与最小项的值.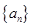 的各项均为正数,且
的各项均为正数,且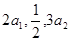 成等差数列,
成等差数列,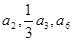 成等比数列.
成等比数列.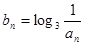 ,记
,记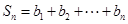 ,
,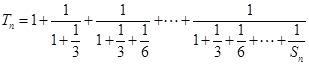 ,求证:
,求证: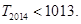
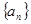 为等差数列,且
为等差数列,且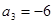 ,
,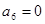 .
.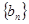 满足
满足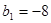 ,
,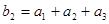 ,求数列
,求数列 项和公式.
项和公式. 是等差数列,
是等差数列, 是等比数列,其中
是等比数列,其中 ,
,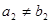 ,且
,且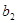 为
为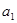 、
、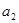 的等差中项,
的等差中项,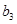 的等差中项.
的等差中项.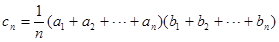 ,求数列
,求数列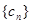 的前
的前 项和
项和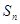 .
.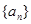 是正数组成的数列,其前
是正数组成的数列,其前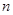 项和为
项和为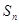 ,且对所有的正整数
,且对所有的正整数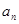 与2的等差中项等于
与2的等差中项等于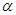 为锐角,且
为锐角,且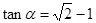 ,函数
,函数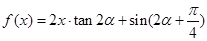 ,数列
,数列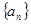 的首项
的首项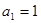 ,
, .
.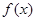 的表达式;(2)求数列
的表达式;(2)求数列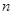 项和
项和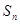 .
.