题目内容
∫-22|x2-x|dx的值为 .
【答案】分析:先根据定积分的几何意义,将原式化成:∫-2(x2-x)dx+∫1(x-x2)dx+∫12(x2-x)dx,再利用定积分的运算法则,找出被积函数的原函数,进行计算即可.
解答:解:原式
=∫-2(x2-x)dx+∫1(x-x2)dx+∫12(x2-x)dx
=( x3-
x3- x2)|-2+(-
x2)|-2+(- x3+
x3+ x2)|1+(
x2)|1+(  x3-
x3- x2)|12
x2)|12
=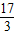 .
.
故答案为: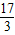 .
.
点评:本题主要考查定积分的基本运算,解题关键是找出被积函数的原函数,利用区间去绝对值符号也是注意点,本题属于基础题.
解答:解:原式
=∫-2(x2-x)dx+∫1(x-x2)dx+∫12(x2-x)dx
=(
 x3-
x3- x2)|-2+(-
x2)|-2+(- x3+
x3+ x2)|1+(
x2)|1+(  x3-
x3- x2)|12
x2)|12=
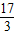 .
.故答案为:
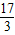 .
.点评:本题主要考查定积分的基本运算,解题关键是找出被积函数的原函数,利用区间去绝对值符号也是注意点,本题属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目