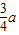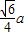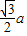题目内容
将∠B=60°,边长为1的菱形ABCD沿对角线AC折成二面角θ,若θ∈[60°,120°],则折后两条对角线之间的距离的最值为( )
A、最小值为
| ||||||
B、最小值为
| ||||||
C、最小值为
| ||||||
D、最小值为
|
分析:折后两条对角线之间的距离的范围可以根据二面角θ的范围求得,故先找出二面角的平面角,取AC的中点E,连接BE、DE,则∠BED=θ,且BE=ED,所以EF⊥BD,再取BD的中点F,由AF=CF可得:EF⊥AC,则折后两条对角线之间的距离为EF的长,所以当θ=120°时,EF取最小值;当θ=60°时,EF取最大值.
解答: 解:由题设∠BED=θ,E、F分别是中点
解:由题设∠BED=θ,E、F分别是中点
则折后两条对角线之间的距离为EF的长
在△BED中,∠BED=θ,BE=DE=
当θ=120°时,EF的最小值为
,
当θ=60°时,EF的最大值为
.
 解:由题设∠BED=θ,E、F分别是中点
解:由题设∠BED=θ,E、F分别是中点则折后两条对角线之间的距离为EF的长
在△BED中,∠BED=θ,BE=DE=
| ||
| 2 |
当θ=120°时,EF的最小值为
| ||
| 4 |
当θ=60°时,EF的最大值为
| 3 |
| 4 |
点评:本小题主要考查空间线面关系、二面角的度量等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,最大值为
,最大值为

 ,最大值为
,最大值为