题目内容
 函数
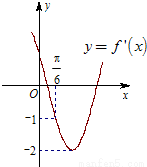
函数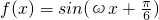 的导函数y=f'(x)的部分图象如图所示:图象与y轴交点
的导函数y=f'(x)的部分图象如图所示:图象与y轴交点 ,与x轴正半轴的两交点为A、C,B为图象的最低点,则S△ABC=________.
,与x轴正半轴的两交点为A、C,B为图象的最低点,则S△ABC=________.

分析:先利用导数的运算性质,求函数f(x)的导函数f′(x),ω,求出函数的周期,即可求解三角形的面积.
解答:∵函数
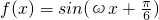 的导函数y=f′(x)=ωcos(ωx+
的导函数y=f′(x)=ωcos(ωx+ ),
),导函数y=f'(x)的图象与y轴交点
 ,∴ωcos
,∴ωcos =
=
∴ω=3,T=
 ,所以三角形的面积为:
,所以三角形的面积为: =
=
故答案为
 .
.点评:本题考查函数与导函数的关系,导函数的图象的应用,注意导函数的图象求三角形的面积.

练习册系列答案
相关题目
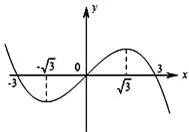 设三次函数f(x)的导函数为f′(x),函数y=x•f′(x)的图象的一部分如图所示,则正确的是( )
设三次函数f(x)的导函数为f′(x),函数y=x•f′(x)的图象的一部分如图所示,则正确的是( )A、f(x)的极大值为f(
| ||||
B、f(x)的极大值为f(-
| ||||
| C、f(x)的极大值为f(-3),极小值为f(3) | ||||
| D、f(x)的极大值为f(3),极小值为f(-3) |
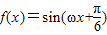 的导函数y=f'(x)的部分图象如图所示:图象与y轴交点
的导函数y=f'(x)的部分图象如图所示:图象与y轴交点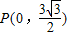 ,与x轴正半轴的交点为A、C,B为图象的最低点,则函数y=f'(x)在点C处的切线方程为 .
,与x轴正半轴的交点为A、C,B为图象的最低点,则函数y=f'(x)在点C处的切线方程为 .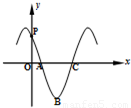
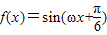 的导函数y=f'(x)的部分图象如图所示:图象与y轴交点
的导函数y=f'(x)的部分图象如图所示:图象与y轴交点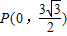 ,与x轴正半轴的交点为A、C,B为图象的最低点,则函数y=f'(x)在点C处的切线方程为 .
,与x轴正半轴的交点为A、C,B为图象的最低点,则函数y=f'(x)在点C处的切线方程为 .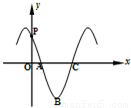
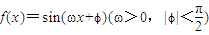 的导函数y=f'(x)的部分图象如图所示,且导函数f'(x)有最小值-2,则ω= ,ϕ= .
的导函数y=f'(x)的部分图象如图所示,且导函数f'(x)有最小值-2,则ω= ,ϕ= .