题目内容
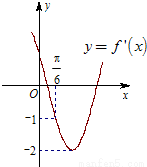
函数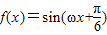
的导函数y=f'（x）的部分图象如图所示：图象与y轴交点
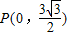，与x轴正半轴的交点为A、C，B为图象的最低点，则函数y=f'（x）在点C处的切线方程为 ．注：（f[g（x）]）′=f′[g（x）]•g′（x）
【答案】分析：求出导函数，利用图象与y轴交点
，求得ω，从而可得函数的解析式，进而可得函数y=f'（x）在点C处的切线斜率，利用点斜式，可得切线方程．
解答：解：由题意，y=f′（x）=ω
∵导函数图象与y轴交点
，
∴ωcos
=
，∴ω=3
∴y=f′（x）=3
令f′（x）=0，可得
即
，从而k=1时，得C（
）
又y′=
∴x=
时，y′=9
∴函数y=f'（x）在点C处的切线方程为y=9（x-
），即9x-y-4π=0．
故答案为：9x-y-4π=0．
点评：本题考查导数知识的运用，考查导数的几何意义，正确求出导函数是关键．
，求得ω，从而可得函数的解析式，进而可得函数y=f'（x）在点C处的切线斜率，利用点斜式，可得切线方程．解答：解：由题意，y=f′（x）=ω
∵导函数图象与y轴交点
，∴ωcos
=，∴ω=3∴y=f′（x）=3
令f′（x）=0，可得
即
，从而k=1时，得C（）又y′=
∴x=
时，y′=9∴函数y=f'（x）在点C处的切线方程为y=9（x-
），即9x-y-4π=0．故答案为：9x-y-4π=0．
点评：本题考查导数知识的运用，考查导数的几何意义，正确求出导函数是关键．
练习册系列答案
相关题目
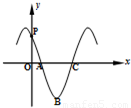
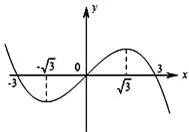设三次函数f（x）的导函数为f′（x），函数y=x•f′（x）的图象的一部分如图所示，则正确的是（ ）A、f（x）的极大值为f(
| ||||
B、f（x）的极大值为f(-
| ||||
| C、f（x）的极大值为f（-3），极小值为f（3） | ||||
| D、f（x）的极大值为f（3），极小值为f（-3） |
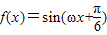的导函数y=f'（x）的部分图象如图所示：图象与y轴交点
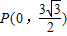，与x轴正半轴的交点为A、C，B为图象的最低点，则函数y=f'（x）在点C处的切线方程为 ．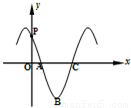
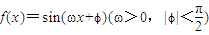的导函数y=f'（x）的部分图象如图所示，且导函数f'（x）有最小值-2，则ω= ，ϕ= ．