题目内容
若函数y=3|x|(x∈[a,b])的值域为[1,9],则a2+b2-2a的取值范围是( )A.[8,12]
B.

C.[4,12]
D.[2,2
 ]
]
【答案】分析:对函数y=3|x|(x∈[a,b])的值域为[1,9]进行分析,由于值域中有1,故定义域中一定有0,又最大值为9,故自变量至少可以取到2,或-2,由此对参数a,b的取值情况进行探究,求出a2+b2-2a的取值范围
解答:解:由题意,0必须在定义域内,且2与-2至少有一个在定义域内
若b=2,则a∈[-2,0),此时a2+b2-2a=(a-1)2+3∈[4,12]
若a=-2,则b∈(0,2],),此时a2+b2-2a=b2+8∈[8,12]
综上a2+b2-2a的取值范围是[4,12]
故选C.
点评:本题考查指数函数的单调性与特殊点,解题的关键是正确理解函数的值域及定义域,对两个参数的取值作出正确判断从而由参数的范围求出a2+b2-2a的取值范围.本题易因为没有找到分类的标准导致无法求出代数式的取值范围,题后应注意体会一下,本题中分类的标准.
解答:解:由题意,0必须在定义域内,且2与-2至少有一个在定义域内
若b=2,则a∈[-2,0),此时a2+b2-2a=(a-1)2+3∈[4,12]
若a=-2,则b∈(0,2],),此时a2+b2-2a=b2+8∈[8,12]
综上a2+b2-2a的取值范围是[4,12]
故选C.
点评:本题考查指数函数的单调性与特殊点,解题的关键是正确理解函数的值域及定义域,对两个参数的取值作出正确判断从而由参数的范围求出a2+b2-2a的取值范围.本题易因为没有找到分类的标准导致无法求出代数式的取值范围,题后应注意体会一下,本题中分类的标准.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
若函数y=2cosωx在区间[0,
]上递减,且有最小值1,则ω的值可以是( )
| 2π |
| 3 |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
若函数y=3|x|(x∈[a,b])的值域为[1,9],则a2+b2-2a的取值范围是( )
| A、[8,12] | ||||
B、[2
| ||||
| C、[4,12] | ||||
D、[2,2
|

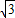 ]
]