题目内容
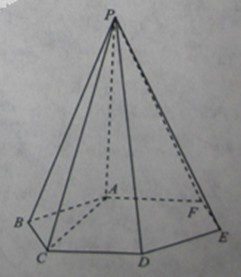
如图,六棱锥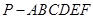 的底面是边长为1的正六边形,
的底面是边长为1的正六边形,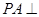 底面
底面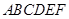 。
。
(Ⅰ)求证:平面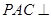 平面
平面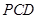 ;
;
(Ⅱ)若直线PC与平面PDE所成角的正弦值为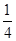 ,求六棱锥
,求六棱锥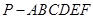 高的大小。
高的大小。
【答案】
(Ⅰ)详见解析;(Ⅱ)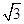
【解析】
试题分析:(Ⅰ)由线线垂直得到线面垂直CD⊥平面PAC,进而求证出面面垂直;(Ⅱ)设AP=h,求出平面PDE的一个法向量,再由线面成角的正弦值得到关于h的方程,解出即可.
试题解析:(Ⅰ)在正六边形ABCDEF中,CD⊥AC.
因为PA⊥底面ABCDEF,CDÌ平面ABCDEF,所以CD⊥PA.
又AC∩PA=A,所以CD⊥平面PAC.
因为CDÌ平面PCD,所以平面PAC⊥平面PCD.

(Ⅱ)如图,分别以AC,AF,AP为x轴,y轴,z轴,建立空间直角坐标系A-xyz.
设AP=h(h>0).
则P(0,0,h),C(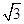 ,0,0),D(
,0,0),D(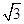 ,1,0),E(
,1,0),E(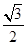 ,
,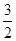 ,0).
,0).
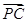 =(
=(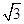 ,0,-h),
,0,-h), =(
=(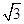 ,1,-h),
,1,-h),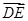 =(-
=(-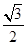 ,
,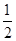 ,0).
,0).
设面PDE的一个法向量为n=(x,y,z),则n· =0,n·
=0,n·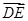 =0,
=0,
所以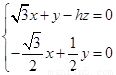 取n=(h,
取n=(h,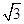 h,2
h,2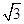 ).
).
记直线PC与平面PDE所成的角为θ,则
sinθ=|cosá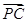 ,nñ|=
,nñ|=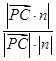 =
=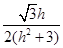 ,
,
由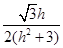 =
=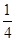 ,解得h=
,解得h=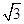 .
.
所以六棱锥P-ABCDEF高为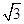 .
.
考点:1、面面垂直的求证;2、向量法求线面成角.

练习册系列答案
相关题目
 A.
A. 
 A.
A.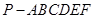 的底面是边长为1的正六边形,
的底面是边长为1的正六边形, 底面
底面 。
。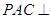 平面
平面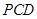 ;
;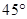 ,求三棱锥
,求三棱锥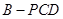 高的大小。
高的大小。