题目内容
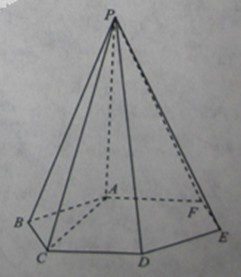
如图,六棱锥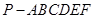 的底面是边长为1的正六边形,
的底面是边长为1的正六边形, 底面
底面 。
。
(Ⅰ)求证:平面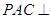 平面
平面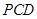 ;
;
(Ⅱ)若直线PC与平面PDE所成角为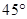 ,求三棱锥
,求三棱锥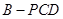 高的大小。
高的大小。

【答案】
(Ⅰ)详见解析;(Ⅱ)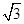
【解析】
试题分析:(Ⅰ)由线线垂直得到线面垂直CD⊥平面PAC,进而求证出面面垂直; (Ⅱ)由已知条件求出S△PCD和S△BCD,再利用等体积法求出三棱锥B-PCD的高.
试题解析:(Ⅰ)在正六边形ABCDEF中,CD⊥AC.
因为PA⊥底面ABCDEF,CDÌ平面ABCDEF,所以CD⊥PA.
又AC∩PA=A,所以CD⊥平面PAC.
因为CDÌ平面PCD,所以平面PAC⊥平面PCD.

(Ⅱ)直线PC与底面ABCDEF所成的角∠PCA=45°.
在Rt△PAC中,AC=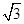 ,所以PA=
,所以PA=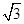 ,PC=
,PC=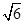 ,
,
即三棱锥P-BCD的高为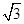 ,
,
S△PCD=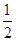 PC·CD=
PC·CD=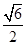 ,S△BCD=
,S△BCD=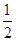 BC·CD sin120°=
BC·CD sin120°=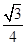 ,
,
设三棱锥B-PCD高为h,由VP-BCD=VB-PCD,得:
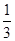 S△BCD·PA=
S△BCD·PA=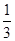 S△PCD·h,
S△PCD·h,
经计算可得:h=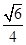 ,
,
所以三棱锥B-PCD高为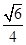 .
.
考点:1、面面垂直的求证;2、线面成角.

练习册系列答案
相关题目
 A.
A. 
 A.
A.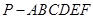 的底面是边长为1的正六边形,
的底面是边长为1的正六边形,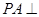 底面
底面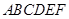 。
。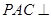 平面
平面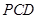 ;
;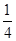 ,求六棱锥
,求六棱锥