题目内容
(已知数列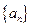 是等差数列,
是等差数列, 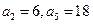 ;数列
;数列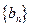 的前n项和是
的前n项和是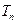 ,且
,且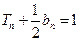 .
.
(Ⅰ) 求数列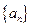 的通项公式;
的通项公式;
(Ⅱ) 求证:数列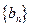 是等比数列;
是等比数列;
(Ⅲ) 记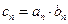 ,求
,求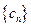 的前n项和
的前n项和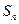 .
.
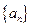 是等差数列,
是等差数列, 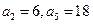 ;数列
;数列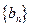 的前n项和是
的前n项和是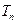 ,且
,且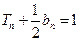 .
.(Ⅰ) 求数列
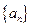 的通项公式;
的通项公式; (Ⅱ) 求证:数列
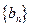 是等比数列;
是等比数列;(Ⅲ) 记
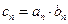 ,求
,求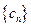 的前n项和
的前n项和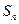 .
.解:(1)设数列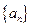 的首项为
的首项为 ,公差为
,公差为 .则有
.则有
 解得
解得
所以数列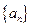 的通项公式为
的通项公式为
(2)当 时,由
时,由 及
及 得
得
当 时, 由
时, 由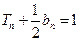 ①
①
知 ②
②
①-②得:

即:
因此,数列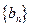 是等比数列,首项为
是等比数列,首项为 ,公比为
,公比为 。
。
(3)由(2)知数列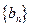 是等比数列,且首项为
是等比数列,且首项为 ,公比为
,公比为 。
。



 ①
①
 ②
②
①-②得

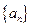 的首项为
的首项为 ,公差为
,公差为 .则有
.则有 解得
解得
所以数列
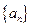 的通项公式为
的通项公式为
(2)当
 时,由
时,由 及
及 得
得
当
 时, 由
时, 由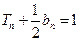 ①
①知
 ②
②①-②得:

即:

因此,数列
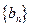 是等比数列,首项为
是等比数列,首项为 ,公比为
,公比为 。
。(3)由(2)知数列
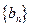 是等比数列,且首项为
是等比数列,且首项为 ,公比为
,公比为 。
。


 ①
① ②
②①-②得

略

练习册系列答案
相关题目
 ……
……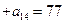 ,且
,且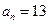
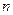 值;(Ⅱ)若
值;(Ⅱ)若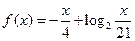 ,求
,求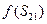 的值
的值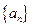 中,若
中,若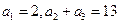 ,则
,则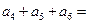
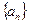 中,若
中,若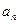 >0,公
>0,公 差
差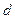 >0,则有
>0,则有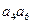 >
>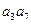 .类比上述性质,在等比数列
.类比上述性质,在等比数列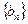 中,若
中,若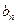 >0,
>0,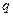 >1,则
>1,则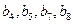 的一个不等关系是 .
的一个不等关系是 .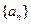 中,
中,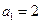 ,
, 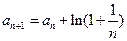 ,则
,则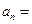 ( )
( ) 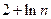
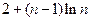
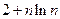
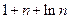
 的前
的前
 项和为
项和为 ,且满足
,且满足 ,则
,则 的值是( )
的值是( )



 ,则
,则 等于( ).
等于( ).

 已知数列-1,
已知数列-1,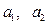 ,
, -4成等差数列,-1,
-4成等差数列,-1, 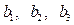 , -4成等比数列,则
, -4成等比数列,则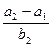 的值
的值 为 ( )
为 ( )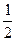 B. -
B. - .
. 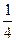
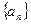 中,
中,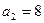 ,前
,前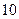 项和
项和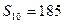
 .
. 通项
通项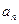 ;
;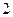 项、第
项、第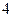 项、第
项、第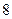 项…第
项…第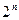 项……按原来的顺序组成一个新的数列
项……按原来的顺序组成一个新的数列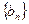 ,求数列
,求数列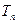 .
.