题目内容
已知数列{an},{bn}满足a1=2,2an=1+anan+1,bn=an-1,数列{bn}的前n项和为Sn,Tn=S2n-Sn.
(Ⅰ)求证:数列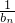 为等差数列,并求通项bn;
为等差数列,并求通项bn;
(Ⅱ)试判断数列{Tn}的单调性,并证明.
(Ⅲ)求证:当n≥2时,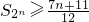 .
.
(Ⅰ)证明:由bn=an-1,得an=bn+1,代入2an=1+anan+1,
得2(bn+1)=1+(bn+1)(bn+1+1),
整理,得bnbn+1+bn+1-bn=0,
从而有 -
- =1,
=1,
∵b1=a1-1=2-1=1,
∴数列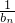 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,
∴ =n,∴bn=
=n,∴bn= ;
;
(Ⅱ)解:数列{Tn}单调递增
∵Sn=1+ +…+
+…+ ,
,
∴Tn=S2n-Sn= +
+ +…+
+…+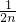 ,
,
∴Tn+1= +
+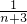 +…+
+…+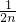 +
+ +
+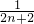 ,
,
∴Tn+1-Tn= +
+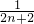 -
- >
>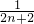 +
+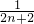 -
- =0,
=0,
∴Tn+1>Tn,
∴数列{Tn}单调递增;
(Ⅲ)证明:①当n=2时, ,结论成立;
,结论成立;
②设n=k时,结论成立,即1+ +…+
+…+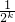 ≥
≥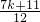 ,
,
则n=k+1时,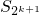 =1+
=1+ +…+
+…+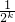 +
+ +…+
+…+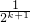 ≥
≥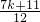 +
+ +…+
+…+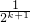 >
>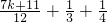 =
=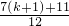 ,即n=k+1时,结论成立
,即n=k+1时,结论成立
∴当n≥2时,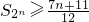 .
.
分析:(I)将两个已知等式结合得到关于数列{bn}的项的递推关系,构造新数列,利用等差数列的通项公式求出 ,进一步求出bn.
,进一步求出bn.
(II)表示出Tn,Tn+1,求出Tn+1-Tn,通过放缩法,判断出此差的符号,判断出Tn+1,Tn两者的大小,即可得到结论;
(Ⅲ)利用数学归纳法证明即可.
点评:本题考查了数列和不等式的综合应用,考查数列的通项,考查数列的单调性,考查不等式的证明,综合性强.
得2(bn+1)=1+(bn+1)(bn+1+1),
整理,得bnbn+1+bn+1-bn=0,
从而有
 -
- =1,
=1,∵b1=a1-1=2-1=1,
∴数列
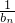 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,∴
 =n,∴bn=
=n,∴bn= ;
;(Ⅱ)解:数列{Tn}单调递增
∵Sn=1+
 +…+
+…+ ,
,∴Tn=S2n-Sn=
 +
+ +…+
+…+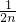 ,
,∴Tn+1=
 +
+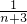 +…+
+…+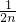 +
+ +
+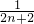 ,
,∴Tn+1-Tn=
 +
+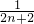 -
- >
>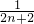 +
+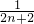 -
- =0,
=0,∴Tn+1>Tn,
∴数列{Tn}单调递增;
(Ⅲ)证明:①当n=2时,
 ,结论成立;
,结论成立;②设n=k时,结论成立,即1+
 +…+
+…+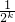 ≥
≥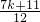 ,
,则n=k+1时,
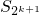 =1+
=1+ +…+
+…+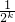 +
+ +…+
+…+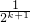 ≥
≥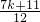 +
+ +…+
+…+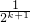 >
>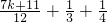 =
=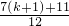 ,即n=k+1时,结论成立
,即n=k+1时,结论成立∴当n≥2时,
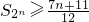 .
.分析:(I)将两个已知等式结合得到关于数列{bn}的项的递推关系,构造新数列,利用等差数列的通项公式求出
 ,进一步求出bn.
,进一步求出bn.(II)表示出Tn,Tn+1,求出Tn+1-Tn,通过放缩法,判断出此差的符号,判断出Tn+1,Tn两者的大小,即可得到结论;
(Ⅲ)利用数学归纳法证明即可.
点评:本题考查了数列和不等式的综合应用,考查数列的通项,考查数列的单调性,考查不等式的证明,综合性强.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目