题目内容
已知双曲线与椭圆
+
=1的焦点重合,它们的离心率之和为
,求双曲线的方程.
| x2 |
| 25 |
| y2 |
| 9 |
| 14 |
| 5 |
分析:设出双曲线方程,求出椭圆的离心率,可得双曲线的离心率,即可确定双曲线的几何性质,从而可得双曲线的方程.
解答:解:设双曲线的方程为
-
=1(a>0,b>0)(3分)
椭圆
+
=1的半焦距c=
=4,离心率为
,(6分)
两个焦点为(4,0)和(-4,0)(9分)
∴双曲线的两个焦点为(4,0)和(-4,0),离心率e=
-
=2
∴
=
=2,∴a=2(12分)
∴b2=c2-a2=12(14分)
∴双曲线的方程为
-
=1(15分)
| x2 |
| a2 |
| y2 |
| b2 |
椭圆
| x2 |
| 25 |
| y2 |
| 9 |
| 25-9 |
| 4 |
| 5 |
两个焦点为(4,0)和(-4,0)(9分)
∴双曲线的两个焦点为(4,0)和(-4,0),离心率e=
| 14 |
| 5 |
| 4 |
| 5 |
∴
| c |
| a |
| 4 |
| a |
∴b2=c2-a2=12(14分)
∴双曲线的方程为
| x2 |
| 4 |
| y2 |
| 12 |
点评:本题双曲线的标准方程,考查椭圆、双曲线的几何性质,考查学生的计算能力,属于中档题.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
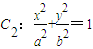 有公共焦点F1F2,点
有公共焦点F1F2,点 是它们的一个公共点.
是它们的一个公共点.