题目内容
已知△ABC的内角A、B、C的对边分别为a、b、c，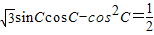
，且c=3．（1）求角C；
（2）若向量
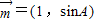与
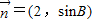共线，求a、b的值．
【答案】分析：（1）利用二倍角公式及辅助角公式对已知化简可得sin（2C-30°）=1，结合C的范围可求C
（2）由（1）C，可得A+B，结合向量共线的坐标表示可得sinB-2sinA=0，利用两角差的正弦公式化简可求
解答：解：（1）∵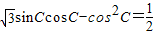
，
∴
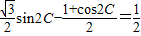
∴sin（2C-30°）=1
∵0°＜C＜180°
∴C=60°
（2）由（1）可得A+B=120°
∵
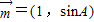与
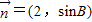共线，
∴sinB-2sinA=0
∴sin（120°-A）=2sinA
整理可得，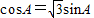
即tanA=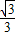
∴A=30°，B=90°
∵c=3．
∴a=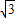
，b=2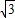
点评：本题主要考查了二倍角公式、辅助角公式及两角和的正弦公式、锐角三角函数的综合应用
（2）由（1）C，可得A+B，结合向量共线的坐标表示可得sinB-2sinA=0，利用两角差的正弦公式化简可求
解答：解：（1）∵
，∴
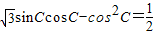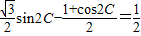
∴sin（2C-30°）=1
∵0°＜C＜180°
∴C=60°
（2）由（1）可得A+B=120°
∵
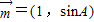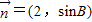与共线，∴sinB-2sinA=0
∴sin（120°-A）=2sinA
整理可得，
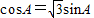即tanA=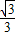∴A=30°，B=90°
∵c=3．
∴a=
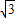，b=2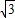点评：本题主要考查了二倍角公式、辅助角公式及两角和的正弦公式、锐角三角函数的综合应用
练习册系列答案
相关题目