题目内容
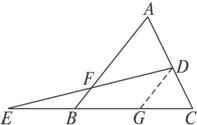
已知△ABC，D、E、F分别在边BC、CA、AB上，且有BD∶DC=AE∶EB=CF∶FA.求证：△DEF与△ABC的重心重合.
思路分析：根据三角形的特点建立坐标系，利用重心坐标公式求解.
证明：以B为坐标原点，BC所在直线为x轴，建立平面直角坐标系，如图：
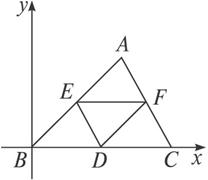
设A(a,b),B(0,0),C(c,0),由重心G(
),设
=λ.
则点D(
0),E(
),F(
).
由重心坐标公式，可知△DEF的重心G′的坐标为：
(
=(
).
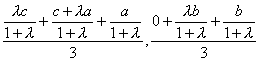∴G与G′重合.也就是△DEF和△ABC的重心重合.
练习册系列答案
相关题目
BC=AC
FD.