题目内容
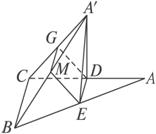
已知△ABC中,D、E分别为AC、AB的中点,沿DE将△ADE折起,使A到A′的位置,M是A′B的中点,求证:ME∥面A′CD.
证明:如图,取A′C的中点G,连结EM、MG、GD.
∵M、G分别是A′B、A′C的中点,
∴MG
BC.同理,DE
BC.
∴MG
DE.
∴四边形DEMG是平行四边形.
∴ME∥DG.
又ME
面A′CD,DG
平面A′CD,
∴ME∥平面A′CD.
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
已知△ABC中,D、E分别为AC、AB的中点,沿DE将△ADE折起,使A到A′的位置,M是A′B的中点,求证:ME∥面A′CD.
证明:如图,取A′C的中点G,连结EM、MG、GD.
∵M、G分别是A′B、A′C的中点,
∴MGBC.同理,DEBC.
∴MGDE.
∴四边形DEMG是平行四边形.
∴ME∥DG.
又ME面A′CD,DG平面A′CD,
∴ME∥平面A′CD.
阅读快车系列答案
BC=AC
FD.
=0.