题目内容
已知圆A过点 ,且与圆B:
,且与圆B:
 关于直线
关于直线 对称.
对称.
(1)求圆A的方程;
(2)若HE、HF是圆A的两条切线,E、F是切点,求 的最小值。
的最小值。
(3)过平面上一点 向圆A和圆B各引一条切线,切点分别为C、D,设
向圆A和圆B各引一条切线,切点分别为C、D,设 ,求证:平面上存在一定点M使得Q到M的距离为定值,并求出该定值.
,求证:平面上存在一定点M使得Q到M的距离为定值,并求出该定值.
 ,且与圆B:
,且与圆B:
 关于直线
关于直线 对称.
对称.(1)求圆A的方程;
(2)若HE、HF是圆A的两条切线,E、F是切点,求
 的最小值。
的最小值。(3)过平面上一点
 向圆A和圆B各引一条切线,切点分别为C、D,设
向圆A和圆B各引一条切线,切点分别为C、D,设 ,求证:平面上存在一定点M使得Q到M的距离为定值,并求出该定值.
,求证:平面上存在一定点M使得Q到M的距离为定值,并求出该定值. (1)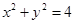 (2)
(2)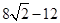 (3)
(3)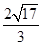
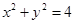 (2)
(2)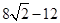 (3)
(3)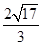
试题分析:(1)求圆的方程即找到圆心和半径. 由圆的标准方程可看出圆B的圆心, 圆A 与圆B 关于直线对称可求出圆A的圆心.再由圆A 通过过点
 通过两点距离公式求出半径可求出圆A的标准方程.
通过两点距离公式求出半径可求出圆A的标准方程.(2) 求
 的最小值最好用一个变量来表示,
的最小值最好用一个变量来表示,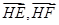 表示长度和夹角都与
表示长度和夹角都与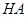 长度有关,所以设
长度有关,所以设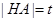 ,则由切割弦定理得
,则由切割弦定理得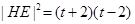 ,在直角三角形
,在直角三角形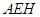 中
中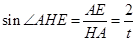 ,则由二倍角公式可得
,则由二倍角公式可得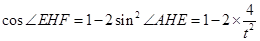 ,由数量积公式得
,由数量积公式得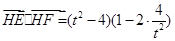 ,利用均值定理可求出最小值.
,利用均值定理可求出最小值.(3)切线长
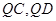 用
用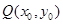 到点
到点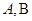 距离和半径表示出来,再根据
距离和半径表示出来,再根据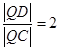 得到关于
得到关于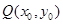 一个方程
一个方程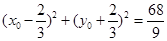 可知
可知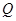 轨迹是一个圆,所以存在一个定点
轨迹是一个圆,所以存在一个定点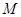 到
到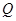 的距离为定值.
的距离为定值.试题解析:
(1)设圆A的圆心A(a,b),由题意得:
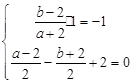 解得
解得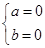 ,
,设圆A的方程为
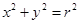 ,将点
,将点 代入得r=2
代入得r=2∴圆A的方程为:
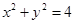 (4分)
(4分)(2)设
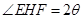 ,
,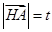 ,
,则
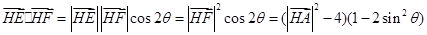
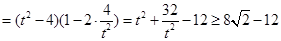
当且仅当
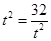 即
即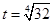 时取等号,∴
时取等号,∴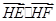 的最小值为
的最小值为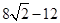 (9分)
(9分)(3)由(1)得圆A的方程为:
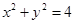 ,圆B:
,圆B: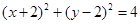 ,由题设得
,由题设得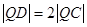 ,即
,即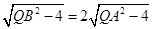 ,
,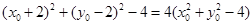 ∴化简得:
∴化简得: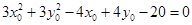
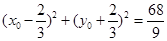 ∴存在定点M(
∴存在定点M(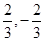 )使得Q到M的距离为定值
)使得Q到M的距离为定值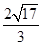 . (14分)
. (14分)
练习册系列答案
相关题目
 ,直线
,直线 .
. 与圆C的位置关系;
与圆C的位置关系;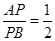 ,求此时直线
,求此时直线 的渐近线与圆
的渐近线与圆 相切,则该双曲线的离心率是__________.
相切,则该双曲线的离心率是__________. 有两个公共点,则实数m的取值范围是_______
有两个公共点,则实数m的取值范围是_______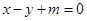 与圆
与圆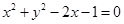 有两个不同交点的一个充分不必要条件是( )
有两个不同交点的一个充分不必要条件是( )



 相交的所有直线中,被圆截得的弦最长时的直线方程是( )
相交的所有直线中,被圆截得的弦最长时的直线方程是( )



 中,圆
中,圆 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 ,则直线
,则直线