题目内容
如图,四棱锥P—ABCD中,底面ABCD是菱形,PA= PD,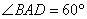 ,E是AD的中点,点Q在侧棱PC上.
,E是AD的中点,点Q在侧棱PC上.
(Ⅰ)求证:AD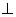 平面PBE;
平面PBE;
(Ⅱ)若Q是PC的中点,求证:PA∥平面BDQ;
(Ⅲ)若 ,试求
,试求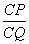 的值.
的值.
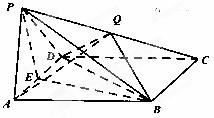
(Ⅰ)证明:由E是AD的中点,PA=PD,所以AD⊥PE ;
又底面ABCD是菱形,∠BAD=600
所以AB=BD,又因为E是AD的中点 ,所以AD⊥BE,
又PE∩BE=E 所以AD⊥平面PBE
(Ⅱ)证明:连接AC交BD于点O,连OQ;因为O是AC的中点,
Q是PC的中点,所以OQ//PA,又PA 平面BDQ,OQ
平面BDQ,OQ 平面BDQ,
平面BDQ,
所以PA//平面BDQ[来源:学§科§网Z§X§X§K]
(Ⅲ)解:设四棱锥P-BCDE,Q-ABCD的高分别为 。
。
所以 ,
,
又因为 ,且底面
,且底面 积
积 ,
,
所以

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
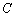 :
: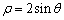 ,过极点O的直线
,过极点O的直线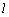 与曲线
与曲线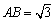 ,求直线
,求直线 满足约束条件
满足约束条件 , 则目标函数
, 则目标函数 的最大值为 .
的最大值为 . 的值的程序框图,其中判断框内应填入的是( )
的值的程序框图,其中判断框内应填入的是( ) B.
B. C.
C. D.
D.

 ,能使方程
,能使方程 两根均为实数的概率为 .
两根均为实数的概率为 . .
. ≤6的解集;
≤6的解集; 的不等式
的不等式 恒成立,求实数
恒成立,求实数 中,若
中,若 ,面积记作
,面积记作 ,则下列结论中一定成立的是
,则下列结论中一定成立的是 B.
B. C.
C. D.
D.
 的值为6,那么运行相应程序,输出的
的值为6,那么运行相应程序,输出的 的值为
的值为 A. 3 B. 5
A. 3 B. 5  上的增函数,若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”的逆否命题为真命题
上的增函数,若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”的逆否命题为真命题 D.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+
D.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+ 1≥0”
1≥0”