题目内容
(本小题满分14分)(理科)已知椭圆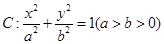 ,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
(1)求椭圆的方程;
(2)过点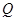
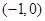 的直线
的直线 交椭圆于
交椭圆于 两点,交直线
两点,交直线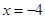 于点
于点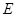 ,且
,且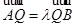 ,
, ,
,
求证: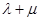 为定值,并计算出该定值.
为定值,并计算出该定值.
(1)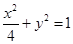 (2)定值为0,证明见解析
(2)定值为0,证明见解析
解析试题分析:(1)由条件得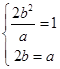 ,解得
,解得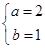 ,所以方程为
,所以方程为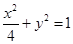 . ……6分
. ……6分
(2)易知直线 斜率存在,令
斜率存在,令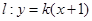 ,
,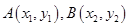
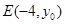 ,
,
由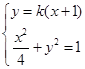 得:
得: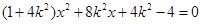 ,
,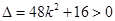 ,
, 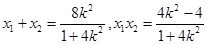 , ……8分
, ……8分
由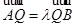 得:
得: ,即
,即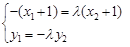 ①
①
由 得:
得: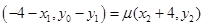 ,即
,即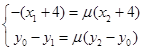 ② ……11分
② ……11分
由①得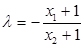 ,由②得
,由②得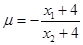 ,
,
∴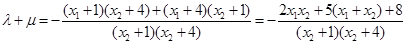 ,
,
将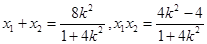 代入有
代入有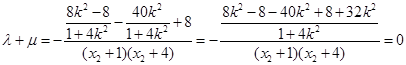 . ……14分
. ……14分
考点:本小题主要考查椭圆方程的求法和椭圆中的定点、定值等综合问题和平面向量知识,考查学生的运算求解能力和数形结合思想.
点评:要想解答好这部分的习题,一方面要掌握好椭圆的标准方程和几何性质等基础知识,另外还要多归纳这些知识的使用方法和应用技巧,做到心中有数,从容应对.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
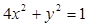 及直线
及直线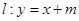 ,当直线和椭圆有公共点时.
,当直线和椭圆有公共点时.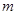 的取值范围;
的取值范围;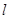 的方程.
的方程.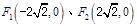 ,长轴长为6,
,长轴长为6,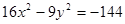 的焦点坐标,离心率和渐近线方程.
的焦点坐标,离心率和渐近线方程. ,
,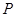 为一个动点,且直线
为一个动点,且直线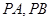 的斜率之积为
的斜率之积为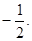
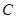 的方程;
的方程;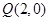 ,过点
,过点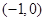 的直线
的直线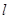 交
交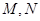 两点,
两点,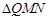 的面积记为S,若对满足条件的任意直线
的面积记为S,若对满足条件的任意直线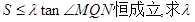 的最小值。
的最小值。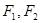 是双曲线
是双曲线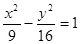 的两个焦点,点
的两个焦点,点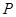 在双曲线上,且
在双曲线上,且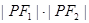
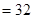 ,求证:
,求证: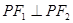
 的两个焦点分别为
的两个焦点分别为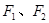 ,离心率为2.
,离心率为2. 的方程;
的方程; 、
、 分别为
分别为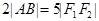 ,求线段
,求线段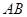 的中点
的中点 的轨迹方程,并说明轨迹是什么曲线;
的轨迹方程,并说明轨迹是什么曲线;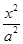 +
+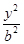 =1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,
=1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,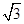 ,
,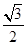 )在椭圆C上,直线l为椭圆C的左准线.
)在椭圆C上,直线l为椭圆C的左准线.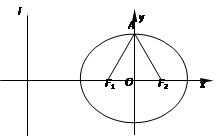
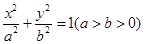 的离心率为
的离心率为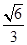 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为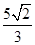 .
.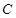 的方程;
的方程;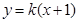 与椭圆
与椭圆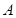 、
、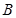 两点.
两点.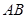 中点的横坐标为
中点的横坐标为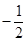 ,求斜率
,求斜率 的值;
的值;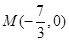 ,求证:
,求证: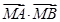 为定值.
为定值.