题目内容
已知向量a=(2cosα,2sinα),b=(3cosβ,3sinβ),a与b的夹角为60°,则直线xcosα-ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1的位置关系是
- A.相切
- B.相交
- C.相离
- D.随α,β的值而定
C
分析:由已知利用向量的数量积的定义可求得cosαcosβ+sinαsinβ= ,要判断直线xcosα-ysinα+1=0与圆的位置关系,只要判断圆心(cosβ,-sinβ)到直线xcosα-ysinα+1=0的距离d=|cosαcosβ+sinαsinβ+1|与圆的半径的比较即可
,要判断直线xcosα-ysinα+1=0与圆的位置关系,只要判断圆心(cosβ,-sinβ)到直线xcosα-ysinα+1=0的距离d=|cosαcosβ+sinαsinβ+1|与圆的半径的比较即可
解答:由题意可得| |=2,
|=2,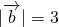 ,
, =
= =2×3×
=2×3× =3
=3
即6cosαcosβ+6sinαsinβ=3
∴cosαcosβ+sinαsinβ=
∵圆心(cosβ,-sinβ)到直线xcosα-ysinα+1=0的距离d=|cosαcosβ+sinαsinβ+1|=
∴直线xcosα-ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相离
故选:C
点评:本题主要考查了向量的数量积的定义及坐标表示,直线与圆的位置关系的判断,综合应用向量,点到直线的距离公式等知识.
分析:由已知利用向量的数量积的定义可求得cosαcosβ+sinαsinβ=
 ,要判断直线xcosα-ysinα+1=0与圆的位置关系,只要判断圆心(cosβ,-sinβ)到直线xcosα-ysinα+1=0的距离d=|cosαcosβ+sinαsinβ+1|与圆的半径的比较即可
,要判断直线xcosα-ysinα+1=0与圆的位置关系,只要判断圆心(cosβ,-sinβ)到直线xcosα-ysinα+1=0的距离d=|cosαcosβ+sinαsinβ+1|与圆的半径的比较即可解答:由题意可得|
 |=2,
|=2,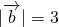 ,
, =
= =2×3×
=2×3× =3
=3即6cosαcosβ+6sinαsinβ=3
∴cosαcosβ+sinαsinβ=

∵圆心(cosβ,-sinβ)到直线xcosα-ysinα+1=0的距离d=|cosαcosβ+sinαsinβ+1|=

∴直线xcosα-ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相离
故选:C
点评:本题主要考查了向量的数量积的定义及坐标表示,直线与圆的位置关系的判断,综合应用向量,点到直线的距离公式等知识.

练习册系列答案
相关题目
已知向量
=(2cosα,2sinα),
=(3cosβ,3sinβ),若向量
与
的夹角为60°,则直线xcosα-ysinα+
=0与圆(x-cosβ)2+(y+sinβ)2=
的位置关系是( )
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| A、相交 | B、相切 |
| C、相离 | D、相交且过圆心 |