题目内容
已知数列![]() (1)求数列
(1)求数列![]() 的通项公式; (2)证明:
的通项公式; (2)证明:![]() ; (3)设
; (3)设![]()
(Ⅰ) ![]() (Ⅱ) 见解析 (Ⅲ)见解析
(Ⅱ) 见解析 (Ⅲ)见解析
解析:
(1)由![]() ,得
,得![]()
令![]() ,有
,有![]() ∴
∴![]()
=![]() =
=![]() 又b1=2a1=2,
又b1=2a1=2,![]()
∴![]() ∴
∴![]() 4分
4分
(2)证法1:(数学归纳法)
1°,当n=1时,a1=1,满足不等式![]()
![]()
![]() 2°,假设n=k(k≥1,k∈N*)时结论成立
2°,假设n=k(k≥1,k∈N*)时结论成立
即![]() ,那么 = 即
,那么 = 即![]()
又![]() 由1°,2°可知,n∈N*,都有
由1°,2°可知,n∈N*,都有![]() 成立 9分
成立 9分
证法2:由⑴知:![]() ∵
∵![]() ,
,![]() ,∴
,∴![]()
∵![]() ∵
∵![]()
∴![]() ∴
∴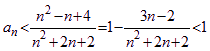
当n=1时,![]() ,综上
,综上![]() 9分
9分
证法3:![]()
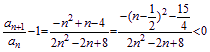
∴![]() 为递减数列
为递减数列
当n=1时,an取最大值 ∴an≤1 由(1)中知![]()
![]()
综上可知![]() 9分
9分
(3)![]()
欲证:![]() 即证
即证![]() 即ln(1+Tn)-Tn<0,构造函数f (x)=ln(1+x)-x
即ln(1+Tn)-Tn<0,构造函数f (x)=ln(1+x)-x
∵![]() 当x>0时,f ' (x)<0
当x>0时,f ' (x)<0
∴函数y=f (x)在(0,+∞)内递减
∴f (x)在[0,+∞)内的最大值为f (0)=0
∴当x≥0时,ln(1+x)-x≤0 又∵Tn>0,∴ln(1+Tn)-Tn<0
∴不等式![]() 成立..14分
成立..14分

练习册系列答案
相关题目

 的通项公式;
的通项公式;

 的通项公式; (2)求证数列
的通项公式; (2)求证数列 是等比数列;
是等比数列; 的集合。
的集合。
 的通项公式; (2)求证数列
的通项公式; (2)求证数列 是等比数列;
是等比数列; 的集合。
的集合。
 的通项公式;
的通项公式; 求数列
求数列 的前n项和
的前n项和

 的通项公式;
的通项公式;