题目内容
 如图,若正方体ABCD-A1B1C1D1的棱长为1,则点C到平面A1BD的距离为
如图,若正方体ABCD-A1B1C1D1的棱长为1,则点C到平面A1BD的距离为分析:利用等体积即Vc-A1BD=VA1-BCD,转化为点C到平面A1BD的距离.
解答:解:构造三棱锥C-A1DB,并且有Vc-A1BD=VA1-BCD,
因为VA1-BCD=
sh=
×
×1×1×1=
,
所以Vc-A1BD=
.
设点C到平面A1BD的距离为x,
又因为Vc-A1BD=
×SA1BD×x=
=
,
所以x=
,即点C到平面A1BD的距离为
.
故答案为
.
因为VA1-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
所以Vc-A1BD=
| 1 |
| 6 |
设点C到平面A1BD的距离为x,
又因为Vc-A1BD=
| 1 |
| 3 |
| ||
| 6 |
| 1 |
| 6 |
所以x=
| ||
| 3 |
| ||
| 3 |
故答案为
| ||
| 3 |
点评:本小题主要考查空间线面关系、点、线、面间的距离计算,利用等体积法求几何体的体积等知识.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则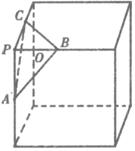
 ,如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记M=
,如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记M= ,N=
,N= ,那么M、N的大小关系是 .
,那么M、N的大小关系是 .