题目内容
(10分)已知直线l:kx-y+1+2k=0.
(1)求证:直线l恒过某个定点;
(2)若直线l交x轴负半轴于A,交y轴正半轴于B,△AOB的面积为S,求S的最小值并求此时直线l的方程;
(1)定点P(-2,1)
(2)求A ,B
,B
S= 后用均值不等式求解
后用均值不等式求解
解析

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
设双曲线  ,离心率
,离心率  ,右焦点
,右焦点  ,方程
,方程  的两个实数根分别为
的两个实数根分别为  ,则点
,则点  与圆
与圆  的位置关系
的位置关系
| A.在圆内 | B.在圆上 | C.在圆外 | D.不确定 |
已知直线l过点(-2,0),当直线l与圆x2+y2=2x有两个交点时,其斜率k的取值范围是( )
A.(-2 ,2 ,2 ) ) | B.(- , , ) ) |
C.(-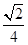 , ,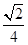 ) ) | D.(-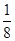 , ,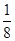 ) ) |
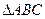 的三个顶点分别为
的三个顶点分别为 ,
,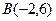 ,
,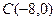
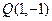 ,直线L的方程是
,直线L的方程是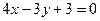 .
.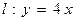 和点
和点 ,点
,点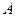 为第一象限内的点且在直线
为第一象限内的点且在直线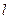 上,直线
上,直线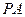 交
交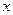 轴正半轴于点
轴正半轴于点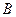 ,求△
,求△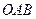 面积的最小值,并求当△
面积的最小值,并求当△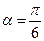 .
.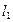 与直线
与直线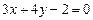 平行且与两坐标轴的正半轴围成的面积为12
平行且与两坐标轴的正半轴围成的面积为12  与直线
与直线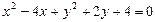 相切,求直线
相切,求直线