题目内容
(1)已知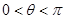 ,
,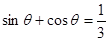 ,求
,求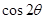 的值;
的值;
(2)已知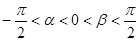 ,
,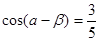 ,
, ,求
,求 的值.
的值.
(1) ;(2)
;(2) .
.
解析试题分析:(1)根据 结合已知条件可知,只需求得
结合已知条件可知,只需求得 的值即可,因此可以考虑将已知等式
的值即可,因此可以考虑将已知等式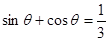 两边平方,得到
两边平方,得到 ,从而
,从而 ,再由
,再由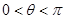 可知
可知 ,从而
,从而 ;(2)已知条件中给出了
;(2)已知条件中给出了 与
与 的三角函数值,结合问题,考虑到
的三角函数值,结合问题,考虑到 ,因此考虑采用两角和的正切公式进行求解,利用同角三角函数的基本关系,结合已知条件中给出的角的范围
,因此考虑采用两角和的正切公式进行求解,利用同角三角函数的基本关系,结合已知条件中给出的角的范围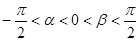 易得
易得 ,
, ,进而求得
,进而求得 .
.
试题解析:(1)∵ ,∴
,∴ , 3分
, 3分
∴ , 4分
, 4分
又∵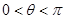 ,∴
,∴ ,
, ,∴
,∴ ,
,
∴ ; 7分
; 7分
(2)∵ 且
且 ,∴
,∴ ,
, , 9分
, 9分
∵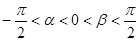 ,∴
,∴ ,
,
又∵ ,∴
,∴ ,∴
,∴ ,
, , 11分
, 11分
∴ . 14分
. 14分
考点:1.同角三角函数基本关系;2.三角恒等变形.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 是方程
是方程 的两个根,则
的两个根,则 的值为 .
的值为 . 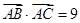 ,sinB= sinCcos
,sinB= sinCcos ,又△ABC的面积为6(Ⅰ)求△ABC的三边长;(Ⅱ)若D为BC边上的一点,且CD=1,求
,又△ABC的面积为6(Ⅰ)求△ABC的三边长;(Ⅱ)若D为BC边上的一点,且CD=1,求 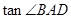 .
. .
. 的值;
的值; 的值.
的值.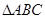 中,内角
中,内角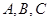 所对的边分别为
所对的边分别为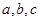 ,且
,且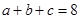
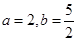 ,求
,求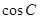 的值;
的值;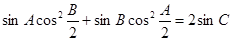 ,且
,且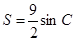 ,求
,求 和
和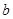 的值.
的值. 分别是角A、B、C的对边,
分别是角A、B、C的对边, ,且
,且 .
. ,且
,且 ,求证:
,求证: .
.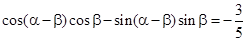 ,
, ,求
,求 的值.
的值. ,则
,则 的值为
的值为