题目内容
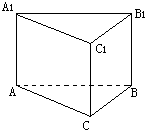（2012•深圳一模）如图，三棱柱ABC-A1B1C1中，AA1⊥平面ABC，A1A=AB=2，BC=1，AC=| 5 |
分析：由题意判断几何体的左视图的图形，利用已知条件的数据关系，求出左视图的面积即可．
解答：解：因为三棱柱ABC-A1B1C1中，AA1⊥平面ABC，所以棱柱是直棱柱，
又A1A=AB=2，BC=1，AC=
，所以AB⊥BC，
在底面ABC中，作BD⊥AC于D，在侧面ACC1A1，中作DD1∥AA1，交A1C1于D1，连结B1D1，
主（正）视方向垂直平面ACC1A1，则此三棱柱的侧（左）视图为矩形BDD1B1，
∴BD=
=
，
侧（左）视图的面积为
×2=
．
故选A．
又A1A=AB=2，BC=1，AC=
| 5 |
在底面ABC中，作BD⊥AC于D，在侧面ACC1A1，中作DD1∥AA1，交A1C1于D1，连结B1D1，
主（正）视方向垂直平面ACC1A1，则此三棱柱的侧（左）视图为矩形BDD1B1，
∴BD=
| AB×BC |
| AC |
2
| ||
| 5 |
侧（左）视图的面积为
2
| ||
| 5 |
4
| ||
| 5 |
故选A．
点评：本题考查三视图与几何体直观图的关系，判断几何体的侧视图的形状以及数据值是解题关键．
练习册系列答案
相关题目
