Question

【题目】已知椭圆:的四个顶点恰好是一边长为2，一内角为的菱形的四个顶点.

(1)求椭圆的方程；

(2)若直线交椭圆于两点，在直线上存在点,使得为等边三角形,求的值.

Answer 1

【答案】（1）；（2）或．

【解析】

试题（1）求椭圆标准方程，要确定的值，题中已知四个顶点形成的菱形是确定的，而椭圆的顶点为，因此易得；（2）本小题采取解析几何的基本解法，是等边三角形的条件是三边相等，或两内角为60°，或且，我们采用且，由线段的中垂线与直线相交求得点的坐标，计算，直线与椭圆相交求得点坐标，计算，利用求得值，由于涉及到的垂线．因此对按和分类讨论．

试题解析：(1)因为椭圆:的四个顶点恰好是一边长为2，

一内角为的菱形的四个顶点, 所以,

椭圆的方程为

(2)设,则

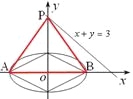
（i）当直线的斜率为0时，的垂直平分线就是轴，轴与直线的交点为,

又，

所以是等边三角形,所以满足条件；

(ii)当直线的斜率存在且不为0时，设的方程为

所以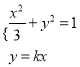，化简得解得

所以

又的中垂线为，它的交点记为

由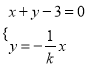解得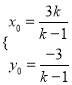

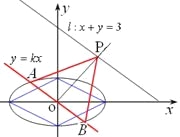
则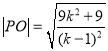

因为为等边三角形， 所以应有

代入得到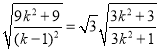，解得（舍），

综上可知，或