题目内容
下图是一个二次函数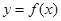
的图象.写出
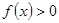的解集；
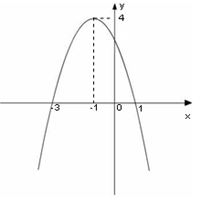
(2)求这个二次函数的解析式；
(3)当实数
在何范围内变化时，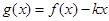
在区间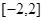 
上是单调函数．
(1) 
(2) 
(3)
或
解析试题分析：（1）由图可知二次函数的零点为
和1，解集为
（2）设二次函数为
,
由点
在函数图像上，得
所以二次函数的解析式为
．
（3）
,开口向下，对称轴为
当
，即时，
在
上递减
当
，即时，在上递增
综上所述或
考点：二次函数求解析式及单调性
点评：解不等式
需找函数图象在x轴上方的部分，二次函数的单调性以对称轴为界，在对称轴的两侧分别为函数的增区间和减区间
练习册系列答案
相关题目
是定义在
上的偶函数，且当
时，
．
的解析式； 
，求函数
的最小值．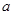
的一块正方形铁皮的四角各截去一个大小相同的小正方形，然后将四边折起做成一个无盖的方盒．欲使所得的方盒有最大容积，截去的小正方形的边长应为多少？方盒的最大容积为多少？
若不建隔热层（即x=0时），每年能源消耗费用为8万元.设f（x）为隔热层建造费用与20年的能源消耗费用之和.
（其中
为大于0的常数），在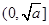
上是减函数，在
上是增函数”这一性质，求隔热层修建多厚时，总费用f(x)达到最小，并求出这个最小值. 
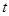表示时间，以月为单位，年初为起点，根据历年数据，某水库的蓄水量（单位：亿立方米）关于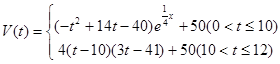
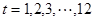）,问：同一年内哪些月份是枯水期？
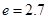计算）
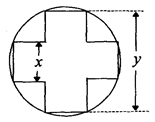
.已知甲、乙两地相距100千米。
的面积，问应如何设计十字型宽
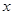及长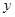
，才能使其外接圆的周长最短，这样可使绕在铁芯上的铜线最节省．