题目内容
已知点![]() 是函数
是函数![]() 且
且![]() )的图象上一点,等比数列
)的图象上一点,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]()
![]() 的首项为
的首项为![]() ,且前
,且前![]() 项和
项和![]() 满足
满足![]() (
(![]() ).
).
(Ⅰ)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 前
前![]() 项和为
项和为![]() ,问满足
,问满足![]() 的最小正整数
的最小正整数![]() 是多少?
是多少?
(Ⅰ)![]()
![]() (Ⅱ)最小正整数为
(Ⅱ)最小正整数为![]()
解析:
(Ⅰ)![]() , ………………………1分
, ………………………1分
![]()

又数列![]() 成等比数列,
成等比数列,

又公比
所以![]()
![]() ; …… 4分
; …… 4分
![]()
![]()
又![]() ,
,![]() ,
, ![]() ;
;
数列![]() 构成一个首相为
构成一个首相为![]() 公差为
公差为![]() 的等差数列,
的等差数列,
![]() ,
, ![]() ……… 6分
……… 6分
当![]() ,
, ![]() ;
;
又![]() 适合上式,
适合上式,![]() (
(![]() ); …………………………8分
); …………………………8分
(Ⅱ)![]()
![]()
………… 11分
![]()
![]() ; …………… 10分
; …………… 10分
由
满足![]() 的最小正整数为
的最小正整数为![]() . …………………… 12分
. …………………… 12分

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
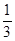 )是函数
)是函数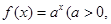 且
且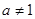 )的图象上一点,等比数列
)的图象上一点,等比数列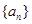 的前
的前 项和为
项和为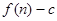 ,数列
,数列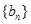
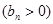 的首项为
的首项为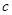 ,且前
,且前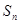 满足
满足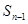 =
=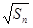 +
+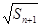 (
(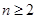 ).
).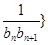 前
前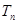 ,问
,问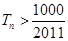 的最小正整数
的最小正整数 是函数
是函数 且
且 )的图象上一点,等比数列
)的图象上一点,等比数列 的前
的前 项和为
项和为 ,数列
,数列
 的首项为
的首项为 ,且前
,且前 满足
满足
 前
前 ,问
,问 的最小正整数
的最小正整数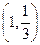 是函数
是函数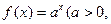 且
且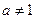 )的图象上一点,等比数列
)的图象上一点,等比数列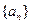 的前
的前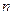 项和为
项和为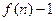 ,数列
,数列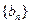
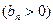 的首项为
的首项为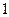 ,且前
,且前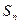 满足
满足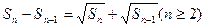
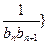 前
前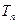 ,问
,问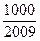 的最小正整数
的最小正整数