题目内容
将等边△OAB的边AB与等腰直角△ABC的斜边AB对接,若
=x
+y
,则x的取值为( )
| OC |
| OA |
| OB |
分析:如图所示:设等边△OAB的边AB=1,则 AC=BC=
,求出点C的坐标为(
,
),根据
=x
+y
,解方程求得x的取值.
| ||
| 2 |
3+
| ||
| 4 |
1+
| ||
| 4 |
| OC |
| OA |
| OB |
解答:解:如图所示:设等边△OAB的边AB=1,则 AC=BC=
.
点C的横坐标为 1+ACcos75°=1+
cos(45°+30°)=1+
(
-
)=
.
点C的纵坐标为ACsin75°=
sin(45°+30°)=
(
+
)=
.
又
=(1,0),
(
,
),
=x
+y
,
∴(
,
)=x•(1,0)+y•(
,
)=(x+
,
y ),
∴
=x+
,
=
y,解得 x=
,y=
.
故选:B.

| ||
| 2 |
点C的横坐标为 1+ACcos75°=1+
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
3+
| ||
| 4 |
点C的纵坐标为ACsin75°=
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
1+
| ||
| 4 |
又
| OA |
| OB |
| 1 |
| 2 |
| ||
| 2 |
| OC |
| OA |
| OB |
∴(
3+
| ||
| 4 |
1+
| ||
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| y |
| 2 |
| ||
| 2 |
∴
3+
| ||
| 4 |
| y |
| 2 |
1+
| ||
| 4 |
| ||
| 2 |
3+
| ||
| 6 |
3+
| ||
| 6 |
故选:B.

点评:本题主要考查两个向量的加减法的法则,以及其几何意义,求出点C的坐标为(
,
),是解题的关键.
3+
| ||
| 4 |
1+
| ||
| 4 |

练习册系列答案
相关题目
 =x
=x +y
+y ,则x的取值为
,则x的取值为
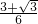


 =x
=x +y
+y ,则x的取值为( )
,则x的取值为( )


