题目内容
若 f(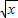 -1)=x-2
-1)=x-2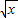 ,则f(x)= .
,则f(x)= .
【答案】分析:可令t=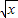 -1则t≥-1且x=(t+1)2然后将x代入到f(
-1则t≥-1且x=(t+1)2然后将x代入到f(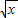 -1)=x-2
-1)=x-2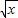 中求出f(t)即求出了f(x),但要标明定义域.
中求出f(t)即求出了f(x),但要标明定义域.
解答:解:∵f(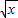 -1)=x-2
-1)=x-2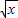
∴令t=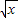 -1则t≥-1且x=(t+1)2
-1则t≥-1且x=(t+1)2
∴f(t)=t2-1(t≥-1)
∴f(x)=x2-1(x≥-1)
故答案为f(x)=x2-1(x≥-1)
点评:本题主要考查了利用换元法求函数的解析式,属常考题,较易.解题的关键是令t=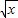 -1然后求出f(t),但要注意t的范围!
-1然后求出f(t),但要注意t的范围!
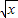 -1则t≥-1且x=(t+1)2然后将x代入到f(
-1则t≥-1且x=(t+1)2然后将x代入到f(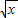 -1)=x-2
-1)=x-2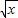 中求出f(t)即求出了f(x),但要标明定义域.
中求出f(t)即求出了f(x),但要标明定义域.解答:解:∵f(
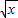 -1)=x-2
-1)=x-2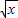
∴令t=
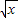 -1则t≥-1且x=(t+1)2
-1则t≥-1且x=(t+1)2∴f(t)=t2-1(t≥-1)
∴f(x)=x2-1(x≥-1)
故答案为f(x)=x2-1(x≥-1)
点评:本题主要考查了利用换元法求函数的解析式,属常考题,较易.解题的关键是令t=
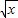 -1然后求出f(t),但要注意t的范围!
-1然后求出f(t),但要注意t的范围! 
练习册系列答案
相关题目
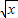 -1)=x-2
-1)=x-2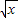 ,则f(x)= .
,则f(x)= .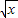 -1)=x-2
-1)=x-2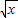 ,则f(x)= .
,则f(x)= .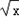 ﹣1)=x﹣2
﹣1)=x﹣2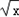 ,则f(x)=( ).
,则f(x)=( ).