题目内容
【题目】已知直线![]() ,椭圆
,椭圆![]() 分别为椭圆的左、右焦点.
分别为椭圆的左、右焦点.
(1)当直线![]() 过右焦点
过右焦点![]() 时,求椭圆
时,求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 为坐标原点,且
为坐标原点,且![]() ,若点
,若点![]() 在以线段
在以线段![]() 为直径的圆内,求实数
为直径的圆内,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出直线![]() 与
与![]() 轴的交点坐标
轴的交点坐标![]() ,可得
,可得![]() ,再由椭圆的方程可得
,再由椭圆的方程可得![]() ,联立方程可求出
,联立方程可求出![]() ,从而可得椭圆
,从而可得椭圆![]() 的标准方程;
的标准方程;
(2) 设![]() ,
,![]() ,联立直线
,联立直线![]() 的方程与椭圆的方程消去
的方程与椭圆的方程消去![]() ,由判别式
,由判别式![]() 求出
求出![]() 的范围,再利用根与系数关系求出
的范围,再利用根与系数关系求出![]() 和
和![]() ,根据
,根据![]() ,可得
,可得![]() ,
,![]() ,其中点坐标
,其中点坐标![]() ,由两点间距离公式可得
,由两点间距离公式可得![]() ,又点
,又点![]() 在以线段
在以线段![]() 为直径的圆内,故
为直径的圆内,故![]() ,即
,即![]() ,把
,把![]() 和
和![]() 结果代入,即可求出实数
结果代入,即可求出实数![]() 的取值范围.
的取值范围.
解:(1)由已知可得直线![]() 与
与![]() 轴的交点坐标
轴的交点坐标![]() ,所以
,所以![]() ①,
①,
又![]() ②,由①②解得
②,由①②解得![]() ,
,![]() ,
,
所以椭圆C的方程为![]() .
.
(2)设![]() ,
,![]() ,
,
由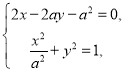 得
得![]() ,
,
由![]() ,又
,又![]() ,解得
,解得![]() ①,
①,
由根与系数关系,得![]() ,
,![]()
由![]() ,
,![]() 可得
可得![]() ,
,![]() ,
,
![]() ,
,
设![]() 是
是![]() 的中点,则
的中点,则![]() ,
,
由已知可得![]() ,即
,即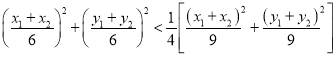 ,
,
整理得![]() ,
,
又![]() ,
,
所以![]() ,
,
所以![]() ,
,
即![]() ,
,
即![]() ,所以
,所以![]() ②,
②,
综上所述,由①②得a的取值范围为![]() .
.

 金钥匙试卷系列答案
金钥匙试卷系列答案【题目】近年来,共享单车在我国各城市迅猛发展,为人们的出行提供了便利,但也给城市的交通管理带来了一些困难,为掌握共享单车在![]() 省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的
省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的![]() 指标
指标![]() 和
和![]() 指标
指标![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并说明
,并说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则认为
,则认为![]() 与
与![]() 具有较强的线性相关关系,否则认为没有较强的线性相关关系).
具有较强的线性相关关系,否则认为没有较强的线性相关关系).
(2)建立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标为7时,
指标为7时,![]() 指标的估计值.
指标的估计值.
(3)若某城市的共享单车![]() 指标
指标![]() 在区间
在区间![]() 的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至
的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至![]() 指标
指标![]() 在区间
在区间![]() 内现已知
内现已知![]() 省某城市共享单车的
省某城市共享单车的![]() 指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
参考公式:回归直线![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为
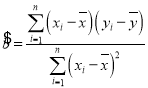 ,,
,,![]() 相关系数
相关系数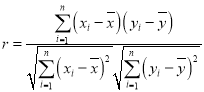
参考数据: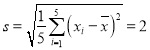 ,
,![]() ,
,![]() .
.