Question

【题目】已知 , ，求直角顶点C的轨迹方程。

Answer 1

【答案】【解答】解：以所在直线为x轴,的中点为坐标原点,建立如图所示的直角坐标系,则有,,设顶点

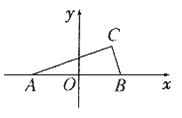
法一：由是直角三角形可知 ,即 ,化简得 ,依题意可知
故所求直角顶点 C的轨迹方程为
法二：由 是直角三角形可知 ,所以 ,则 ,化简得直角顶点C 的轨迹方程为
法三：由是直角三角形可知,且点C与点B不重合,所以 ,化简得直角顶点C的轨迹方程为
【解析】本题主要考查了平面直角坐标系与曲线方程，解决问题的关键是需要结合几何图形的结构特点,建立适当的平面直角坐标系,然后设出所求动点的坐标,寻找满足几何关系的等式,化简后即可得到所求的轨迹方程；
求轨迹方程，其实质就是根据题假设条件，把几何关系通过“坐标”转化成代数关系，得到对应的方程、(1)求轨迹方程时的一般步骤是：建系 设点 列式 化简 检验；(2)求轨迹方程时注意不要把范围扩大或缩小，也就是要检验轨迹的纯粹性和完备性；(3)由于观察的角度不同，因此探求关系的方法也不同，解题时要善于从对角度思考问题