题目内容
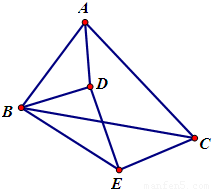
已知：在△ABC内任取一点D，连接AD，BD，点E在△ABC外，∠EBC=∠ABD，∠ECB=∠DAB，求证：△DBE∽△ABC．
证明：∵∠EBC=∠ABD，∠ECB=∠DAB 可得，△ABD∽△CBE．
∴
=
，∴
=
．
故在△DBE 和△ABC中，∠ABC=∠DBE，且此角的两边对应成比例．
∴△DBE∽△ABC．
∴
| BE |
| BD |
| BC |
| AB |
| BE |
| BC |
| BD |
| AB |
故在△DBE 和△ABC中，∠ABC=∠DBE，且此角的两边对应成比例．
∴△DBE∽△ABC．
练习册系列答案
相关题目
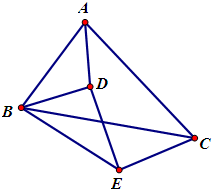已知：在△ABC内任取一点D，连接AD，BD，点E在△ABC外，∠EBC=∠ABD，∠ECB=∠DAB，求证：△DBE∽△ABC．
已知：在△ABC内任取一点D，连接AD，BD，点E在△ABC外，∠EBC=∠ABD，∠ECB=∠DAB，求证：△DBE∽△ABC．