题目内容
如图，两个全等的正方形
ABCD和ABEF所在平面相交于AB，
，
，且AM=FN．求证：MN∥平面BCE．
答案：略
解析：
提示：
解析：
|
证法一：如图，作 MP∥AB交BC于P，NQ∥AB交BE于Q，∴ MP∥NQ，∵AM＝FN，∴ ， ．
∴ MP NQ，则四边形MNQP为平行四边形，∴MN∥PQ，
∵  平面BCE， 平面BCE，∴MN∥平面BCE．
证法二：如图，连结 AN并延长，交BE的延长线于G，连结CG，∵ AF∥BG，∴ ，∴MN∥CG，
∵
|
平面BCE，
平面BCE，∴MN∥平面BCE．
提示：
|
要证线面平行，须找线线平行． |
练习册系列答案
相关题目
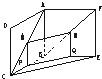如图，两个全等的正方形ABCD和ABEF所在平面相交于AB，M∈AC，N∈FB且AM=FN，求证：MN∥平面BCE．
，
，且AM=FN．求证：MN∥平面BCE．
