题目内容
已知函数 的图象为曲线C,函数
的图象为曲线C,函数 的图象为直线l.
的图象为直线l.
(Ⅰ) 设m>0,当x∈(m,+∞)时,证明:
(Ⅱ) 设直线l与曲线C的交点的横坐标分别为x1,x2,且x1≠x2,求证:(x1+x2)g(x1+x2)>2.
 的图象为曲线C,函数
的图象为曲线C,函数 的图象为直线l.
的图象为直线l.(Ⅰ) 设m>0,当x∈(m,+∞)时,证明:

(Ⅱ) 设直线l与曲线C的交点的横坐标分别为x1,x2,且x1≠x2,求证:(x1+x2)g(x1+x2)>2.
证明:(1)令H(x)=(x+m)ln ﹣2(x﹣m),x∈(m,+∞),
﹣2(x﹣m),x∈(m,+∞),
则H(m)=0,
要证明(x+m)ln ﹣2(x﹣m)>0,
﹣2(x﹣m)>0,
只需证H(x)=(x+m)ln ﹣2(x﹣m)>H(m),
﹣2(x﹣m)>H(m),
∵H′(x)=ln +
+ ﹣1,
﹣1,
令G(x)=ln +
+ ﹣1,G′(x)=
﹣1,G′(x)= ﹣
﹣ ,
,
由G′(x)= >0得,x>m,
>0得,x>m,
∴G(x)在x∈(m,+∞)单调递增,
∴G(x)>G(m)=0
H'(x)>0,H(x)在x∈(m,+∞)单调递增.
H(x)>H(m)=0,
∴H(x)=(x+m)ln ﹣2(x﹣m)>0,
﹣2(x﹣m)>0,
(2)不妨设0<x1<x2,
要证(x1+x2)g(x1+x2)>2,
只需证(x1+x2)[ a(x1+x2)+b]>2,
a(x1+x2)+b]>2,
只需证(x1+x2)[ a
a +bx2﹣(
+bx2﹣( a
a +bx1)]>2(x2﹣x1),
+bx1)]>2(x2﹣x1),
∵ =
= ax1+b,
ax1+b, =
= ax2+b,
ax2+b,
即(x1+x2)ln >2(x2﹣x1)(*),
>2(x2﹣x1)(*),
而由(1)知(*)成立.
所以(x1+x2)g(x1+x2)>2
 ﹣2(x﹣m),x∈(m,+∞),
﹣2(x﹣m),x∈(m,+∞),则H(m)=0,
要证明(x+m)ln
 ﹣2(x﹣m)>0,
﹣2(x﹣m)>0,只需证H(x)=(x+m)ln
 ﹣2(x﹣m)>H(m),
﹣2(x﹣m)>H(m),∵H′(x)=ln
 +
+ ﹣1,
﹣1,令G(x)=ln
 +
+ ﹣1,G′(x)=
﹣1,G′(x)= ﹣
﹣ ,
,由G′(x)=
 >0得,x>m,
>0得,x>m,∴G(x)在x∈(m,+∞)单调递增,
∴G(x)>G(m)=0
H'(x)>0,H(x)在x∈(m,+∞)单调递增.
H(x)>H(m)=0,
∴H(x)=(x+m)ln
 ﹣2(x﹣m)>0,
﹣2(x﹣m)>0,(2)不妨设0<x1<x2,
要证(x1+x2)g(x1+x2)>2,
只需证(x1+x2)[
 a(x1+x2)+b]>2,
a(x1+x2)+b]>2,只需证(x1+x2)[
 a
a +bx2﹣(
+bx2﹣( a
a +bx1)]>2(x2﹣x1),
+bx1)]>2(x2﹣x1),∵
 =
= ax1+b,
ax1+b, =
= ax2+b,
ax2+b,即(x1+x2)ln
 >2(x2﹣x1)(*),
>2(x2﹣x1)(*),而由(1)知(*)成立.
所以(x1+x2)g(x1+x2)>2

练习册系列答案
相关题目
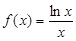 的图象为曲线
的图象为曲线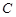 , 函数
, 函数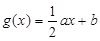 的图象为直线
的图象为直线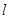 .
.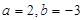 时, 求
时, 求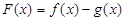 的最大值;
的最大值;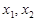 , 且
, 且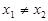 ,
,  .
. 的图象为曲线C。
的图象为曲线C。 轴平行,求
轴平行,求 的关系;
的关系; 时取得极值,求此时
时取得极值,求此时 的取值范围。
的取值范围。