题目内容
(本小题满分14分)
在数列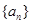 中,
中, 为其前
为其前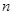 项和,满足
项和,满足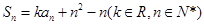 .
.
(1)若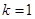 ,求数列
,求数列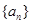 的通项公式;
的通项公式;
(2)若数列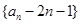 为公比不为1的等比数列,求
为公比不为1的等比数列,求
(1) (2)
(2)
解析试题分析:解:(1)当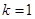 时,
时, 所以
所以 ,即
,即 ……3分所以当
……3分所以当 时,
时, ;当
;当 时,
时, 所以数列
所以数列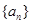 的通项公式为
的通项公式为 …6分
…6分
(2)当 时,
时, ,
, ,
, ,若
,若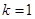 ,则
,则 ,
,
从而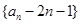 为公比为1的等比数列,不合题意;
为公比为1的等比数列,不合题意;
若 ,则
,则 ,
, ,
,

由题意得, ,所以
,所以 或
或 .
.
当 时,
时, ,得
,得 ,
, ,不合题意;
,不合题意;
当 时,
时, ,从而
,从而
因为
 ,
, 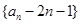 为公比为3的等比数列,
为公比为3的等比数列, ,所以
,所以 ,从而
,从而 .
.
考点:数列的通项公式和求和
点评:解决的关键是能结合前n项和与通项公式的关系来求解通项公式,同时结合等比数列的求和公式得到结论,属于基础题。

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
已知正项数列{an}的前n项和为Sn,且a1=1,an= +
+ (n≥2),则数列{an}的通项公式为an=( )
(n≥2),则数列{an}的通项公式为an=( )
| A.n-1 | B.n | C.2n-1 | D.2n |
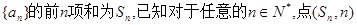 都在函数
都在函数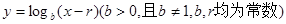 的图象上。
的图象上。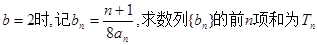 ;
;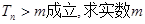 的取值范围。
的取值范围。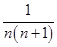 .
.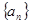 的通项公式为
的通项公式为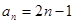 ,数列
,数列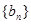 的前n项和为
的前n项和为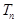 ,且满足
,且满足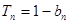
 中是否存在使得
中是否存在使得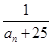 是
是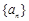 的前n项和为
的前n项和为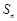 ,点
,点 均在直线
均在直线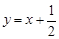 上.
上. 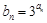 ,试证明数列
,试证明数列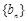 为等比数列.
为等比数列.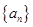 的前n项和为
的前n项和为 ,且满足
,且满足 ,n=1,2,3,…….
,n=1,2,3,……. 满足
满足 ,且
,且 ,求数列
,求数列 ,求数列
,求数列 的前n项和
的前n项和 .
.
 <0.001成立的最小的n值.
<0.001成立的最小的n值. 的前
的前 项和为
项和为 ,且
,且
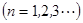 ,等差数列
,等差数列 中,
中, ,
,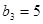 。
。 的通项
的通项 和
和 ;
; ,求数列
,求数列 的前
的前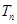 ,
,