题目内容

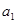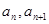已知=2，点（）在函数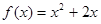的图像上，其中=.

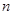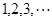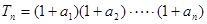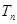（1）设，求及数列{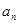}的通项公式；

（2）记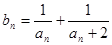，求数列{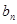}的前n项和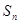，并求.

【解析】本试题主要考查了数列的通项公式和数列求和的运用。注意构造等比数列的思想的运用。并能运用裂项求和。

 

【答案】

（1）证明：由已知，

两边取对数得，即

是公比为2的等比数列。

（2）解：由（1）知=

（3）

又

又

 

练习册系列答案
相关题目
已知定义在R上的函f（x）的图象关于点（-
3
4
，0）对称，且满足f（x）=-f（x+
3
2
），f（0）=2，f（1）=-1，则f（1）+f（2）+f（3）+…+f（2009）的值是（　　）
A、1B、-1C、2D、-2
已知函f（x）=x2-8lnx，g（x）=-x2+14x
（1）求函数f（x）在点（1，f（1））处的切线方程；
（2）若函数f（x）与g（x）在区间（a，a+1）上均为增函数，求a的取值范围；
（3）若方程f（x）=g（x）+m有唯一解，试求实数m的值．
已知函f（x）=x3+ax2+bx+5，若x=
23
，y=f（x） 有极值，且曲线y=f（x）在点（1，f（1））处的切线斜率为3．
（1）求函数f（x）的解析式；
（2）求y=f（x）在[-4，1]上的最大值和最小值．
（3）函数y=f（x）-m有三个零点，求实数m的取值范围．
已知函致f （x）=x3+bx2+cx+d．
（I）当b=0时，证明：曲线y=f（x）与其在点（0，f（0））处的切线只有一个公共点；
（Ⅱ）若曲线y=f（x）在点（1，f（1））处的切线为12x+y-13=0，记函数y=f（x）的两个极值点为x1，x2，当x1+x2=2时，求f（x1）+f（x2）．

已知函数，

(1)若函数在[l，+∞]上是增函数，求实数的取值范围。

(2)若=一是的极值点，求在[l，]上的最大值：

(3)在(2)的条件下，是否存在实数b，使得函数g()=b的图像与函的图像恰有3个交点，若存在，求出实数b的取值范围：若不存在，试说明理由。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网