题目内容
已知点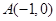 、
、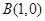 ,
,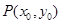 是直线
是直线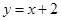 上任意一点,以
上任意一点,以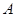 、
、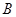 为
为
焦点的椭圆过点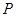 .记椭圆离心率
.记椭圆离心率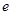 关于
关于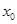 的函数为
的函数为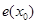 ,那么下列结论正确的是( )
,那么下列结论正确的是( )
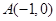 、
、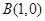 ,
,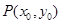 是直线
是直线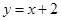 上任意一点,以
上任意一点,以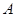 、
、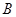 为
为焦点的椭圆过点
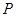 .记椭圆离心率
.记椭圆离心率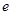 关于
关于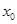 的函数为
的函数为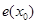 ,那么下列结论正确的是( )
,那么下列结论正确的是( ) A.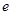 与 与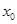 一一对应 一一对应 | B.函数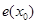 无最小值,有最大值 无最小值,有最大值 |
C.函数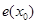 是增函数 是增函数 | D.函数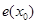 有最小值,无最大值 有最小值,无最大值 |
B
分析:由题意可得c=1,椭圆离心率e=
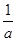 ,由椭圆的定义可得PA+PB=2a,a=
,由椭圆的定义可得PA+PB=2a,a= 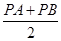 ,再由PA+PB 有最小值而没有最大值,从而得出结论.
,再由PA+PB 有最小值而没有最大值,从而得出结论.解答:由题意可得c=1,椭圆离心率e=
 =
=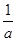 .故当a取最大值时e取最小,a取最小值时e取最大.
.故当a取最大值时e取最小,a取最小值时e取最大.由椭圆的定义可得PA+PB=2a,a=
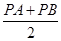 .
.由于PA+PB 有最小值而没有最大值,即a有最小值而没有最大值,
故椭圆离心率e 有最大值而没有最小值,故B正确,且 D不正确.
当直线y=x+2和椭圆相交时,这两个交点到A、B两点的距离之和相等,
都等于2a,故这两个交点对应的离心率e相同,故A不正确.
由于当x0的取值趋于负无穷大时,PA+PB=2a趋于正无穷大;
而当当x0的取值趋于正无穷大时,PA+PB=2a也趋于正无穷大,故函数e(x0)不是增函数,故C不正确.
故选B.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
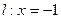 相切。
相切。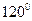 的直线与曲线M相交于A,B两点,A,B在直线
的直线与曲线M相交于A,B两点,A,B在直线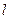 上的射影是
上的射影是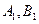 。求梯形
。求梯形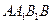 的面积;
的面积;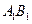 上的动点,当△ABC为直角三角形时,求点C的坐标。
上的动点,当△ABC为直角三角形时,求点C的坐标。 是椭圆
是椭圆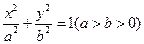 的左、右焦点,过点
的左、右焦点,过点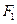 作
作 的直线
的直线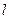 交椭圆于
交椭圆于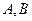 两点,
两点,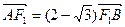 .
.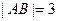 ,求椭圆的标准方程.
,求椭圆的标准方程.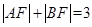 ,则线
,则线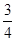
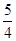
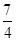
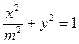 (常数
(常数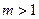 ),P是曲线C上的动点,M是曲线C的右
),P是曲线C上的动点,M是曲线C的右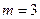 ,求|PA|的最大值与最小值.
,求|PA|的最大值与最小值. 的取值范围.
的取值范围.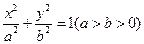 的右焦点
的右焦点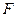 ,其右准线与
,其右准线与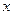 轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点
轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点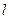 与抛物线
与抛物线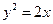 交于点
交于点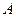 、
、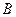 ,以线段
,以线段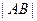 为直径的圆
为直径的圆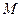 恰与抛物线
恰与抛物线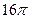 ,则直线
,则直线
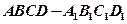 中,
中,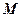 为
为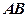 的中点,P是平面
的中点,P是平面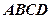 内的动点,且满足条件
内的动点,且满足条件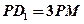 ,则动点P在平面
,则动点P在平面