题目内容
若f(x)=xe-x在x=x0处的切线与x轴平行,则此切线方程是 .
分析:由题意可得导函数,进而得导数值即斜率,求出x0,即可得出切线方程.
解答:解:∵f(x)=xe-x,∴f′(x)=e-x(1-x),
∴f′(x0)=e-x0(1-x0),
∵f(x)=xe-x在x=x0处的切线与x轴平行,
∴e-x0(1-x0)=0,
∴x0=1,
∴f(x0)=f(1)=
,
∴所求切线方程是y=
.
故答案为:y=
.
∴f′(x0)=e-x0(1-x0),
∵f(x)=xe-x在x=x0处的切线与x轴平行,
∴e-x0(1-x0)=0,
∴x0=1,
∴f(x0)=f(1)=
| 1 |
| e |
∴所求切线方程是y=
| 1 |
| e |
故答案为:y=
| 1 |
| e |
点评:本题为切线方程的求解,利用导数求直线的斜率是解决问题的关键,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
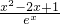 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.